【题目】如下图,在四棱柱![]() 中,点
中,点![]() 分别为
分别为![]() 的中点.
的中点.

(1)求证: ![]() 平面
平面![]() ;
;
(2)若四棱柱![]() 是长方体,且
是长方体,且![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成二面角的正弦值.
所成二面角的正弦值.
参考答案:
【答案】(1)详见解析;(2)![]() .
.
【解析】试题分析:(1)取![]() 的中点为
的中点为![]() ,连结
,连结![]() ,要证线面平行,即证明平面外的线与平面内的线平行,所以证明
,要证线面平行,即证明平面外的线与平面内的线平行,所以证明![]() 是平行四边形,即证明
是平行四边形,即证明![]() ;(2)以点
;(2)以点![]() 为原点,
为原点, ![]() 分别为
分别为![]() 轴建立空间直角坐标系,分别求平面
轴建立空间直角坐标系,分别求平面![]() 和平面
和平面![]() 的法向量,求法向量夹角的余弦值,再求正弦值.
的法向量,求法向量夹角的余弦值,再求正弦值.
试题解析:(1)设![]() 的中点为
的中点为![]() ,连接
,连接![]() 、
、![]() .
.
∵![]() 为
为![]() 的中点,∴
的中点,∴![]() ,且
,且![]() .
.
又∵![]() 为四棱柱
为四棱柱![]() 的棱
的棱![]() 的中点,
的中点,
∴![]() ,且
,且![]() ,
,
∴四边形![]() 是平行四边形.∴
是平行四边形.∴![]() .
.
又∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
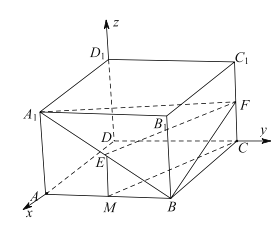
(2)根据四棱柱![]() 是长方体,建立如图所示的空间直角坐标系
是长方体,建立如图所示的空间直角坐标系![]() ,设
,设![]() ,由已知得
,由已知得![]() .
.
![]() ,设平面
,设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则![]() .
.
∴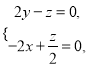 取
取![]() ,解得
,解得![]()
∴![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
由已知容易得到![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
设平面![]() 与平面
与平面![]() 所成二面角的大小为
所成二面角的大小为![]() ,则
,则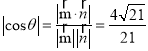 .
.
∵![]() ,∴
,∴![]() .
.
∴平面![]() 与平面
与平面![]() 所成二面角的正弦值为
所成二面角的正弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 的顶点为原点
的顶点为原点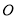 ,焦点为圆
,焦点为圆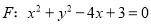 的圆心
的圆心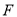 .经过点
.经过点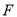 的直线
的直线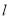 交抛物线
交抛物线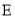 于
于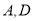 两点,交圆
两点,交圆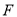 于
于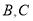 两点,
两点, 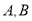 在第一象限,
在第一象限, 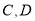 在第四象限.
在第四象限.(1)求抛物线
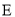 的方程;
的方程;(2)是否存在直线
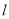 ,使
,使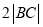 是
是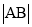 与
与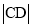 的等差中项?若存在,求直线
的等差中项?若存在,求直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前项n和为Sn , 且3Sn=4an﹣4.又数列{bn}满足bn=log2a1+log2a2+…+log2an .
(1)求数列{an}、{bn}的通项公式;
(2)若 ,求使得不等式
,求使得不等式  恒成立的实数k的取值范围.
恒成立的实数k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是自然对数的底数,
是自然对数的底数,  ,
,  ,
,  ,
,  .
.(1)设
 ,求
,求 的极值;
的极值;(2)设
 ,求证:函数
,求证:函数 没有零点;
没有零点;(3)若
 ,设
,设 ,求证:
,求证:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( 且
且 ),
), 为自然对数的底数.
为自然对数的底数.(Ⅰ)当
 时,求函数
时,求函数 在区间
在区间 上的最大值;
上的最大值;(Ⅱ)若函数
 只有一个零点,求
只有一个零点,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
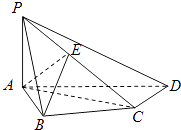
(1)证明CD⊥AE;
(2)证明PD⊥平面ABE;
(3)求二面角A﹣PD﹣C的正切值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=log
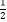 (x2﹣2x)的单调递增区间是( )
(x2﹣2x)的单调递增区间是( )
A.(1,+∞)
B.(2,+∞)
C.(﹣∞,0)
D.(﹣∞,1)
相关试题

