【题目】已知函数![]() .
.
(1)求函数![]() ;
;
(2)设函数![]() ,其中a∈(1,2),求函数g(x)在区间[1,e]上的最小值.
,其中a∈(1,2),求函数g(x)在区间[1,e]上的最小值.
参考答案:
【答案】(1) ![]() 是函数
是函数![]() 的极小值点,极大值点不存在.(2)
的极小值点,极大值点不存在.(2) ![]() 的最小值为
的最小值为![]()
【解析】试题分析:对函数求导,令导数为零,求出![]() 值,划分区间,研究导数在个区间内的符号,得出极值点;写出函数
值,划分区间,研究导数在个区间内的符号,得出极值点;写出函数![]() ,求导得出
,求导得出![]() ,令
,令![]() ,得出
,得出![]() ,研究
,研究![]() 的单调性,根据
的单调性,根据![]() ,得出
,得出![]() 的范围,求出最值.
的范围,求出最值.
试题解析:
(1)函数![]() 的定义域为
的定义域为![]() ,
, ![]() , 由f′(x)=0得
, 由f′(x)=0得![]() ,
,
所以f′(x)在区间![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
所以![]() 是函数
是函数![]() 的极小值点,极大值点不存在.
的极小值点,极大值点不存在.
(2)![]() ,则
,则![]() ,
,
由![]() ,得
,得![]() .
.
所以函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增.
上单调递增.
![]() 当a∈(1,2),
当a∈(1,2),![]()
![]() ,由于
,由于![]() , 当
, 当![]() 时,
时, ![]() 取得最小值
取得最小值
为![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,  边上的中线
边上的中线 长为3,且
长为3,且 ,
,  .
.(1)求
 的值;
的值;(2)求
 及
及 外接圆的面积.
外接圆的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
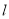 :
: 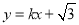 与
与 轴的交点是椭圆
轴的交点是椭圆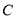 :
: 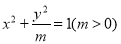 的一个焦点.
的一个焦点.(1)求椭圆
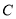 的方程;
的方程;(2)若直线
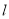 与椭圆
与椭圆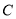 交于
交于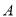 、
、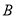 两点,是否存在
两点,是否存在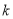 使得以线段
使得以线段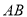 为直径的圆恰好经过坐标原点
为直径的圆恰好经过坐标原点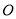 ?若存在,求出
?若存在,求出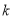 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:向量
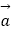 =(1,﹣3),
=(1,﹣3), 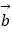 =(﹣2,m),且
=(﹣2,m),且 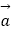 ⊥(
⊥( 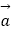 ﹣
﹣ 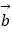 ).
).
(1)求实数m的值;
(2)当k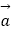 +
+ 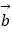 与
与 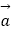 ﹣
﹣ 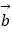 平行时,求实数k的值.
平行时,求实数k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分8分) 已知抛物线C:y=-x2+4x-3 .
(1)求抛物线C在点A(0,-3)和点B(3,0)处的切线的交点坐标;
(2)求抛物线C与它在点A和点B处的切线所围成的图形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
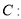
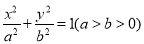 ,
, 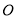 是坐标原点,
是坐标原点,  分别为其左右焦点,
分别为其左右焦点, 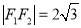 ,
, 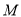 是椭圆上一点,
是椭圆上一点, 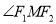 的最大值为
的最大值为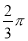
(Ⅰ)求椭圆
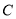 的方程;
的方程;(Ⅱ)若直线
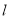 与椭圆
与椭圆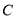 交于
交于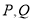 两点,且
两点,且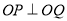
(i)求证:
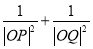 为定值;
为定值;(ii)求
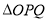 面积的取值范围.
面积的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=Asin(ωx+φ),x∈R(其中
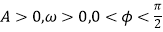 )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为  ,且图象上一个最低点为
,且图象上一个最低点为 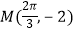 .
.
(1)求f(x)的解析式;
(2)当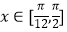 ,求f(x)的值域.
,求f(x)的值域.
相关试题

