【题目】已知椭圆![]()
![]() ,
, ![]() 是坐标原点,
是坐标原点, ![]() 分别为其左右焦点,
分别为其左右焦点, ![]() ,
, ![]() 是椭圆上一点,
是椭圆上一点, ![]() 的最大值为
的最大值为![]()
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]()
(i)求证: ![]() 为定值;
为定值;
(ii)求![]() 面积的取值范围.
面积的取值范围.
参考答案:
【答案】(1)![]() (2)见解析
(2)见解析
【解析】试题分析:(1)由椭圆对称性可得M为短轴端点B时![]() 取最大值,因此根据直角三角形
取最大值,因此根据直角三角形![]() 可得
可得![]() ,(2)(i)解几中证明题一般方法为以算代证,先由直线方程与椭圆方程联立,解出
,(2)(i)解几中证明题一般方法为以算代证,先由直线方程与椭圆方程联立,解出![]() 坐标(用直线斜率表示),代入
坐标(用直线斜率表示),代入![]() 可得定值,最后验证斜率不存在的情况也满足(ii)因为
可得定值,最后验证斜率不存在的情况也满足(ii)因为![]() ,所以
,所以![]() 面积为
面积为![]() ,再将(i)
,再将(i)![]() 坐标(用直线斜率表示)代入,得关于直线斜率的一元函数关系,利用基本不等式求最值,确定函数取值范围.
坐标(用直线斜率表示)代入,得关于直线斜率的一元函数关系,利用基本不等式求最值,确定函数取值范围.
试题解析:(1)由题意得![]() ,得椭圆方程为:
,得椭圆方程为: ![]()
(2)
i)当![]() 斜率都存在且不为0时,设
斜率都存在且不为0时,设![]() ,
, ![]()
由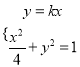 消
消![]() 得
得![]() ,
, ![]()
同理得![]() ,
, ![]()
故![]()
当![]() 斜率一个为0,一个不存在时,得
斜率一个为0,一个不存在时,得![]()
综上得![]() ,得证。
,得证。
ii) 当![]() 斜率都存在且不为0时,
斜率都存在且不为0时,
![]()
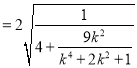
又 ![]()
所以![]()
当![]() 斜率一个为0,一个不存在时,
斜率一个为0,一个不存在时, ![]()
综上得![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:向量
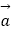 =(1,﹣3),
=(1,﹣3), 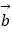 =(﹣2,m),且
=(﹣2,m),且 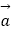 ⊥(
⊥( 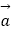 ﹣
﹣ 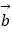 ).
).
(1)求实数m的值;
(2)当k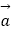 +
+ 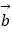 与
与 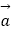 ﹣
﹣ 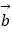 平行时,求实数k的值.
平行时,求实数k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)求函数
 ;
;(2)设函数
 ,其中a∈(1,2),求函数g(x)在区间[1,e]上的最小值.
,其中a∈(1,2),求函数g(x)在区间[1,e]上的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分8分) 已知抛物线C:y=-x2+4x-3 .
(1)求抛物线C在点A(0,-3)和点B(3,0)处的切线的交点坐标;
(2)求抛物线C与它在点A和点B处的切线所围成的图形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=Asin(ωx+φ),x∈R(其中
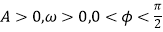 )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为  ,且图象上一个最低点为
,且图象上一个最低点为 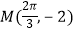 .
.
(1)求f(x)的解析式;
(2)当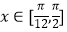 ,求f(x)的值域.
,求f(x)的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
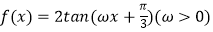 的最小正周期为
的最小正周期为  .
.
(1)求函数f(x)的定义域;
(2)求函数f(x)的单调区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】1979年,李政道博士给中国科技大学少年班出过一道智趣题:5只猴子分一堆桃子,怎么也不能分成5等份,只好先去睡觉,准备第二天再分,夜里1只猴子偷偷爬起来,先吃掉一个桃子,然后将其分成5等份,藏起自己的一份就去睡觉了;第2只猴子又爬起来,将剩余的桃子吃掉一个后,也将桃子分成5等份;藏起自己的一份睡觉去了;以后的3只猴子都先后照此办理,问:最初至少有多少个桃子?最后至少剩下多少个桃子?
相关试题

