【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的普通方程为
的普通方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为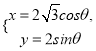 (
(![]() 为参数),设直线
为参数),设直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求线段![]() 的长;
的长;
(Ⅱ)已知点![]() 在曲线
在曲线![]() 上运动,当
上运动,当![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标及
的坐标及![]() 的最大面积.
的最大面积.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ)将曲线![]() 的参数方程化为普通方程,与直线方程联立,求出
的参数方程化为普通方程,与直线方程联立,求出![]() 点的坐标,利用两点间的距离公式求解即可;(Ⅱ)设过点
点的坐标,利用两点间的距离公式求解即可;(Ⅱ)设过点![]() 且与直线
且与直线![]() 平行的直线方程
平行的直线方程![]() .则
.则![]() 与
与![]() 相切时,
相切时, ![]() 的最大面积,求出
的最大面积,求出![]() 点坐标,根据点到直线的距离公式及三角形面积公式可得结果.
点坐标,根据点到直线的距离公式及三角形面积公式可得结果.
试题解析:(Ⅰ)曲线![]() 的普通方程为
的普通方程为![]() .
.
将直线![]() 代入
代入![]() 中消去
中消去![]() 得,
得, ![]() .
.
解得![]() 或
或![]() .
.
所以点![]() ,
, ![]() ,
,
所以![]()
![]() .
.
(Ⅱ)在曲线![]() 上求一点
上求一点![]() ,使
,使![]() 的面积最大,则点
的面积最大,则点![]() 到直线
到直线![]() 的距离最大.
的距离最大.
设过点![]() 且与直线
且与直线![]() 平行的直线方程
平行的直线方程![]() .
.
将![]() 代入
代入![]() 整理得,
整理得, ![]() .
.
令![]()
![]() ,解得
,解得![]() .
.
将![]() 代入方程
代入方程![]() ,解得
,解得![]() .
.
易知当点![]() 的坐标为
的坐标为![]() 时,
时, ![]() 的面积最大.
的面积最大.
且点![]() 到直线
到直线![]() 的距离为
的距离为![]()
![]() .
.
![]() 的最大面积为
的最大面积为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1~4,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图10中有10个直角三角形的内切圆,它们的面积分别记为S1 , S2 , S3 , …,S10 , 则S1+S2+S3+…+S10=

-
科目: 来源: 题型:
查看答案和解析>>【题目】三棱柱
 ,侧棱与底面垂直,
,侧棱与底面垂直, ,
, ,
, ,
, 分别是
分别是 ,
,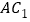 的中点.
的中点.
(
 )求证:
)求证: 平面
平面 .
.(
 )求证:平面
)求证:平面 平面
平面 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 的两条对角线相交于点
的两条对角线相交于点 ,
,  边所在直线的方程为
边所在直线的方程为 ,点
,点 在
在 边所在的直线上.
边所在的直线上.
(Ⅰ)求
 边所在直线的方程;
边所在直线的方程;(Ⅱ)求矩形
 外接圆的方程.
外接圆的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场拟对某商品进行促销,现有两种方案供选择,每种促销方案都需分两个月实施,且每种方案中第一个月与第二个月的销售相互独立.根据以往促销的统计数据,若实施方案1,预计第一个月的销量是促销前的1.2倍和1.5倍的概率分别是0.6和0.4,第二个月的销量是第一个月的1.4倍和1.6倍的概率都是0.5;若实施方案2,预计第一个月的销量是促销前的1.4倍和1.5倍的概率分别是0.7和0.3,第二个月的销量是第一个月的1.2倍和1.6倍的概率分别是0.6和0.4.令
 表示实施方案
表示实施方案 的第二个月的销量是促销前销量的倍数.
的第二个月的销量是促销前销量的倍数.(Ⅰ)求
 ,
,  的分布列;
的分布列;(Ⅱ)不管实施哪种方案,
 与第二个月的利润之间的关系如下表,试比较哪种方案第二个月的利润更大.
与第二个月的利润之间的关系如下表,试比较哪种方案第二个月的利润更大.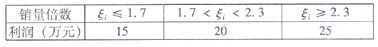
-
科目: 来源: 题型:
查看答案和解析>>【题目】国内某知名连锁店分店开张营业期间,在固定的时间段内消费达到一定标准的顾客可进行一次抽奖活动,随着抽奖活动的有效展开,参与抽奖活动的人数越来越多,该分店经理对开业前7天参加抽奖活动的人数进行统计,
 表示开业第
表示开业第 天参加抽奖活动的人数,得到统计表格如下:
天参加抽奖活动的人数,得到统计表格如下:
经过进一步的统计分析,发现
 与
与 具有线性相关关系.
具有线性相关关系.(1)根据上表给出的数据,用最小二乘法,求出
 与
与 的线性回归方程
的线性回归方程 ;
;(2)若该分店此次抽奖活动自开业始,持续10天,参加抽奖的每位顾客抽到一等奖(价值200元奖品)的概率为
 ,抽到二等奖(价值100元奖品)的概率为
,抽到二等奖(价值100元奖品)的概率为 ,抽到三等奖(价值10元奖品)的概率为
,抽到三等奖(价值10元奖品)的概率为 ,试估计该分店在此次抽奖活动结束时送出多少元奖品?
,试估计该分店在此次抽奖活动结束时送出多少元奖品?参考公式:
 ,
,
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
 中,侧面
中,侧面 底面
底面 ,
, ,
, ,且
,且 ,点
,点 ,
, ,
, 分别为
分别为 ,
, ,
, 的中点.
的中点.
(Ⅰ)求证:
 平面
平面 .
.(Ⅱ)求证:
 平面
平面 .
.(Ⅲ)写出四棱锥
 的体积.(只写出结论,不需要说明理由)
的体积.(只写出结论,不需要说明理由)
相关试题

