【题目】如图,三棱柱![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() ,且
,且![]() ,点
,点![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 的中点.
的中点.

(Ⅰ)求证:![]() 平面
平面![]() .
.
(Ⅱ)求证:![]() 平面
平面![]() .
.
(Ⅲ)写出四棱锥![]() 的体积.(只写出结论,不需要说明理由)
的体积.(只写出结论,不需要说明理由)
参考答案:
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】试题分析:(1)由三线合一得A1D⊥AC,再利用面面垂直的性质得出A1D⊥平面ABC;
(2)取B1C1的中点为G,连结FG,GB,则可证明四边形FGBE为平行四边形,从而EF∥BG,于是EF∥平面BB1C1C;
(3)过A1作A1M⊥CC1,垂足为M,则可证明A1M⊥平面BCC1B1.于是A1M为四棱锥A1﹣BB1C1C的高,底面为矩形,代入体积公式计算即可.
(1)证明:∵![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
在等边![]() 中,
中,
![]() 是边
是边![]() 的中点,
的中点,
∴![]() ,
,
又∵侧面![]() 底面
底面![]() ,
,
侧面![]() 底面
底面![]() .
.
![]() 侧面
侧面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() 中点,
中点,
∴![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() .
.
又∵![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
(3)![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
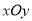 中,已知直线
中,已知直线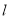 的普通方程为
的普通方程为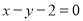 ,曲线
,曲线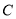 的参数方程为
的参数方程为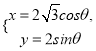 (
(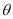 为参数),设直线
为参数),设直线 与曲线
与曲线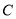 交于
交于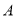 ,
, 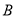 两点.
两点.(Ⅰ)求线段
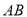 的长;
的长;(Ⅱ)已知点
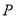 在曲线
在曲线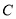 上运动,当
上运动,当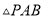 的面积最大时,求点
的面积最大时,求点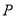 的坐标及
的坐标及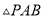 的最大面积.
的最大面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场拟对某商品进行促销,现有两种方案供选择,每种促销方案都需分两个月实施,且每种方案中第一个月与第二个月的销售相互独立.根据以往促销的统计数据,若实施方案1,预计第一个月的销量是促销前的1.2倍和1.5倍的概率分别是0.6和0.4,第二个月的销量是第一个月的1.4倍和1.6倍的概率都是0.5;若实施方案2,预计第一个月的销量是促销前的1.4倍和1.5倍的概率分别是0.7和0.3,第二个月的销量是第一个月的1.2倍和1.6倍的概率分别是0.6和0.4.令
 表示实施方案
表示实施方案 的第二个月的销量是促销前销量的倍数.
的第二个月的销量是促销前销量的倍数.(Ⅰ)求
 ,
,  的分布列;
的分布列;(Ⅱ)不管实施哪种方案,
 与第二个月的利润之间的关系如下表,试比较哪种方案第二个月的利润更大.
与第二个月的利润之间的关系如下表,试比较哪种方案第二个月的利润更大.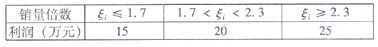
-
科目: 来源: 题型:
查看答案和解析>>【题目】国内某知名连锁店分店开张营业期间,在固定的时间段内消费达到一定标准的顾客可进行一次抽奖活动,随着抽奖活动的有效展开,参与抽奖活动的人数越来越多,该分店经理对开业前7天参加抽奖活动的人数进行统计,
 表示开业第
表示开业第 天参加抽奖活动的人数,得到统计表格如下:
天参加抽奖活动的人数,得到统计表格如下:
经过进一步的统计分析,发现
 与
与 具有线性相关关系.
具有线性相关关系.(1)根据上表给出的数据,用最小二乘法,求出
 与
与 的线性回归方程
的线性回归方程 ;
;(2)若该分店此次抽奖活动自开业始,持续10天,参加抽奖的每位顾客抽到一等奖(价值200元奖品)的概率为
 ,抽到二等奖(价值100元奖品)的概率为
,抽到二等奖(价值100元奖品)的概率为 ,抽到三等奖(价值10元奖品)的概率为
,抽到三等奖(价值10元奖品)的概率为 ,试估计该分店在此次抽奖活动结束时送出多少元奖品?
,试估计该分店在此次抽奖活动结束时送出多少元奖品?参考公式:
 ,
,
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥S-ABCD中,底面ABCD为菱形,SD⊥平面ABCD,点E为SD的中点.
(1)求证:直线SB∥平面ACE
(2)求证:直线AC⊥平面SBD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C是⊙O上一点,∠ACD=∠B,AD⊥CD.
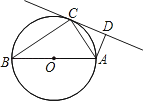
(1)求证:CD是⊙O的切线;
(2)若AD=1,OA=2,求AC的值. -
科目: 来源: 题型:
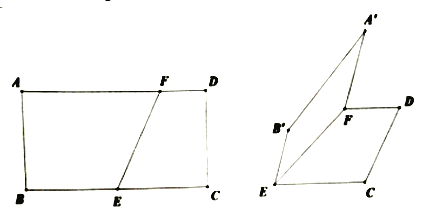
查看答案和解析>>【题目】如图,在矩形
 中,
中,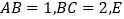 为
为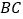 的中点,
的中点,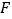 为线段
为线段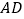 上的一点,且
上的一点,且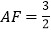 .现将四边形
.现将四边形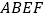 沿直线
沿直线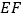 翻折,使翻折后的二面角
翻折,使翻折后的二面角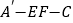 的余弦值为
的余弦值为 .
.
(1)求证:
 ;
;(2)求直线
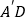 与平面
与平面 所成角的大小.
所成角的大小.
相关试题

