【题目】三棱柱![]() ,侧棱与底面垂直,
,侧棱与底面垂直,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.
的中点.

(![]() )求证:
)求证:![]() 平面
平面![]() .
.
(![]() )求证:平面
)求证:平面![]() 平面
平面![]() .
.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)欲证MN||平面BCC1B1,根据直线与平面平行的判定定理可知只需证MN与平面BCC1B1内一直线平行即可,而连接BC1,AC1.根据中位线定理可知MN||BC1,又MN平面BCC1B1满足定理所需条件;(2)证明MN⊥BC1,MN⊥AC1,即可证明MN⊥平面ABC1,从而证明平面MAC1⊥平面ABC1.
(![]() )连接
)连接![]() ,
,![]() .
.
在![]() 中,∵
中,∵![]() ,
,![]() 是
是![]() ,
,![]() 的中点,
的中点,
∴![]() ,
,
又∵![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(![]() )∵三棱柱
)∵三棱柱![]() 中,侧棱与底面垂直,
中,侧棱与底面垂直,
∴四边形![]() 是正方形,
是正方形,
∴![]() ,
,
∴![]() ,
,
连接![]() ,
,![]() ,则
,则![]() ≌
≌![]() ,
,
∴![]() ,
,
∵![]()
![]() 的中点,
的中点,
∴![]() ,
,
∵![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
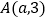 ,圆
,圆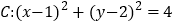 .
.(
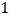 )设
)设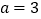 ,求过点
,求过点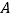 且与圆
且与圆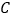 相切的直线方程.
相切的直线方程.(
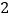 )设
)设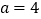 ,直线
,直线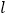 过点
过点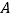 且被圆
且被圆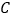 截得的弦长为
截得的弦长为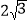 ,求直线
,求直线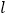 的方程.
的方程.(
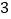 )设
)设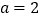 ,直线
,直线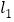 过点
过点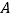 ,求
,求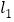 被圆
被圆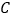 截得的线段的最短长度,并求此时
截得的线段的最短长度,并求此时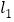 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
(Ⅰ)已知
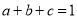 ,证明:
,证明:  ;
;(Ⅱ)若对任意实数
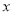 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1~4,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图10中有10个直角三角形的内切圆,它们的面积分别记为S1 , S2 , S3 , …,S10 , 则S1+S2+S3+…+S10=

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 的两条对角线相交于点
的两条对角线相交于点 ,
,  边所在直线的方程为
边所在直线的方程为 ,点
,点 在
在 边所在的直线上.
边所在的直线上.
(Ⅰ)求
 边所在直线的方程;
边所在直线的方程;(Ⅱ)求矩形
 外接圆的方程.
外接圆的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
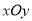 中,已知直线
中,已知直线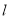 的普通方程为
的普通方程为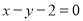 ,曲线
,曲线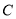 的参数方程为
的参数方程为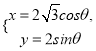 (
(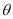 为参数),设直线
为参数),设直线 与曲线
与曲线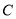 交于
交于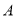 ,
, 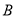 两点.
两点.(Ⅰ)求线段
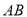 的长;
的长;(Ⅱ)已知点
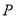 在曲线
在曲线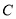 上运动,当
上运动,当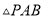 的面积最大时,求点
的面积最大时,求点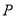 的坐标及
的坐标及 的最大面积.
的最大面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场拟对某商品进行促销,现有两种方案供选择,每种促销方案都需分两个月实施,且每种方案中第一个月与第二个月的销售相互独立.根据以往促销的统计数据,若实施方案1,预计第一个月的销量是促销前的1.2倍和1.5倍的概率分别是0.6和0.4,第二个月的销量是第一个月的1.4倍和1.6倍的概率都是0.5;若实施方案2,预计第一个月的销量是促销前的1.4倍和1.5倍的概率分别是0.7和0.3,第二个月的销量是第一个月的1.2倍和1.6倍的概率分别是0.6和0.4.令
 表示实施方案
表示实施方案 的第二个月的销量是促销前销量的倍数.
的第二个月的销量是促销前销量的倍数.(Ⅰ)求
 ,
,  的分布列;
的分布列;(Ⅱ)不管实施哪种方案,
 与第二个月的利润之间的关系如下表,试比较哪种方案第二个月的利润更大.
与第二个月的利润之间的关系如下表,试比较哪种方案第二个月的利润更大.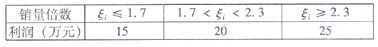
相关试题

