【题目】三棱柱ABC﹣A1B1C1的侧面AA1C1C为正方形,侧面AA1B1B⊥侧面BB1C1C,且AC=2,AB= ![]() ,∠A1AB=45°,E、F分别为AA1、CC1的中点.
,∠A1AB=45°,E、F分别为AA1、CC1的中点. 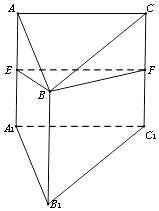
(1)求证:AA1⊥平面BEF;
(2)求二面角B﹣EB1﹣C1的余弦值.
参考答案:
【答案】
(1)证明: ![]() ,∠A1AB=45°,AE=1,故BE⊥AA1.
,∠A1AB=45°,AE=1,故BE⊥AA1.
又AA1∥BB1,故BE⊥BB1,又侧面AA1B1B⊥侧面BB1C1C
故BE⊥平面BB1C1C.EF∥AC,AC⊥AA1,EF⊥AA1,
故AA1⊥平面BEF
(2)解:以BF为x轴,BE为y轴,B1B为z轴,建立空间直角坐标系.
则E(0,1,0),B1(0,0,﹣2), ![]()
平面BEB1的法向量为 ![]() (1,0,0),
(1,0,0),
![]() =(0,﹣1,﹣2),
=(0,﹣1,﹣2), ![]() =(
=( ![]() ,﹣1,﹣1),
,﹣1,﹣1),
设平面EB1C1的法向量 ![]() =(x,y,z),
=(x,y,z),
则 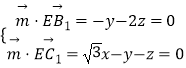 ,
,
取y=2,得 ![]() =
= ![]() ,
,
设二面角B﹣EB1﹣C1的平面角为θ,
则cosθ= ![]() =
= 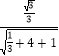 =
= ![]() .
.
∴二面角B﹣EB1﹣C1的余弦值为 ![]() .
.
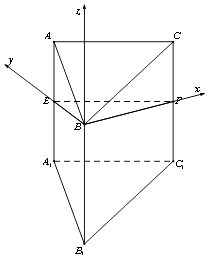
【解析】(1)推导出BE⊥AA1 , BE⊥BB1 , 从而BE⊥平面BB1C1C,由此能证明AA1⊥平面BEF.(2)以BF为x轴,BE为y轴,B1B为z轴,建立空间直角坐标系,利用向量法能求出二面角B﹣EB1﹣C1的余弦值.
【考点精析】通过灵活运用直线与平面垂直的判定,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
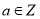 ,已知定义在R上的函数
,已知定义在R上的函数 在区间
在区间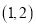 内有一个零点
内有一个零点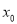 ,
, 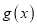 为
为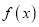 的导函数.
的导函数.(Ⅰ)求
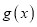 的单调区间;
的单调区间;(Ⅱ)设
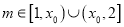 ,函数
,函数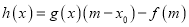 ,求证:
,求证:  ;
;(Ⅲ)求证:存在大于0的常数
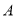 ,使得对于任意的正整数
,使得对于任意的正整数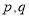 ,且
,且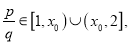 满足
满足 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=3ax2﹣2(a+b)x+b,(0≤x≤1)其中a>0,b为任意常数.
(I)若b= ,f(x)=|x﹣
,f(x)=|x﹣  |在x∈[0,1]有两个不同的解,求实数a的范围.
|在x∈[0,1]有两个不同的解,求实数a的范围.
(II)当|f(0)|≤2,|f(1)|≤2时,求|f(x)|的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】从甲地到乙地要经过3个十字路口,设各路口信号灯工作相互独立,且在各路口遇到红灯的概率分别为
 .
.(Ⅰ)设
 表示一辆车从甲地到乙地遇到红灯的个数,求随机变量
表示一辆车从甲地到乙地遇到红灯的个数,求随机变量 的分布列和数学期望;
的分布列和数学期望;(Ⅱ)若有2辆车独立地从甲地到乙地,求这2辆车共遇到1个红灯的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系xOy中,设椭圆E:
 =1(a>b>0),其中b=
=1(a>b>0),其中b=  a,F为椭圆的右焦点,P(1,1)为椭圆E内一点,PF⊥x轴.
a,F为椭圆的右焦点,P(1,1)为椭圆E内一点,PF⊥x轴. 
(1)求椭圆E的方程;
(2)过P点作斜率为k1 , k2的两条直线分别与椭圆交于点A,C和B,D.若满足|AP||PC|=|BP||DP|,问k1+k2是否为定值?若是,请求出此定值;若不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,曲线y=x2+mx–2与x轴交于A,B两点,点C的坐标为(0,1).当m变化时,解答下列问题:
(1)能否出现AC⊥BC的情况?说明理由;
(2)证明过A,B,C三点的圆在y轴上截得的弦长为定值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四面体ABCD中,△ABC是正三角形,AD=CD.

(1)证明:AC⊥BD;
(2)已知△ACD是直角三角形,AB=BD.若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.
相关试题

