【题目】如图,四面体ABCD中,△ABC是正三角形,AD=CD.

(1)证明:AC⊥BD;
(2)已知△ACD是直角三角形,AB=BD.若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.
参考答案:
【答案】(1)见解析;(2)1:1.
【解析】试题分析:(1)取![]() 的中点
的中点![]() ,由等腰三角形及等边三角形的性质得
,由等腰三角形及等边三角形的性质得![]() ,
, ![]() ,再根据线面垂直的判定定理得
,再根据线面垂直的判定定理得![]() 平面
平面![]() ,即得AC⊥BD;(2)先由AE⊥EC,结合平面几何知识确定
,即得AC⊥BD;(2)先由AE⊥EC,结合平面几何知识确定![]() ,再根据锥体的体积公式得所求体积之比为1:1.
,再根据锥体的体积公式得所求体积之比为1:1.
试题解析: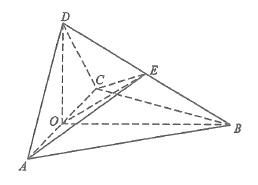
(1)取AC的中点O,连结DO,BO.
因为AD=CD,所以AC⊥DO.
又由于![]() 是正三角形,所以AC⊥BO.
是正三角形,所以AC⊥BO.
从而AC⊥平面DOB,故AC⊥BD.
(2)连结EO.
由(1)及题设知∠ADC=90°,所以DO=AO.
在![]() 中,
中, ![]() .
.
又AB=BD,所以
![]() ,故∠DOB=90°.
,故∠DOB=90°.
由题设知![]() 为直角三角形,所以
为直角三角形,所以![]() .
.
又![]() 是正三角形,且AB=BD,所以
是正三角形,且AB=BD,所以![]() .
.
故E为BD的中点,从而E到平面ABC的距离为D到平面ABC的距离的![]() ,四面体ABCE的体积为四面体ABCD的体积的
,四面体ABCE的体积为四面体ABCD的体积的![]() ,即四面体ABCE与四面体ACDE的体积之比为1:1.
,即四面体ABCE与四面体ACDE的体积之比为1:1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三棱柱ABC﹣A1B1C1的侧面AA1C1C为正方形,侧面AA1B1B⊥侧面BB1C1C,且AC=2,AB=
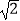 ,∠A1AB=45°,E、F分别为AA1、CC1的中点.
,∠A1AB=45°,E、F分别为AA1、CC1的中点. 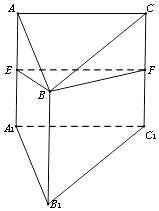
(1)求证:AA1⊥平面BEF;
(2)求二面角B﹣EB1﹣C1的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系xOy中,设椭圆E:
 =1(a>b>0),其中b=
=1(a>b>0),其中b=  a,F为椭圆的右焦点,P(1,1)为椭圆E内一点,PF⊥x轴.
a,F为椭圆的右焦点,P(1,1)为椭圆E内一点,PF⊥x轴. 
(1)求椭圆E的方程;
(2)过P点作斜率为k1 , k2的两条直线分别与椭圆交于点A,C和B,D.若满足|AP||PC|=|BP||DP|,问k1+k2是否为定值?若是,请求出此定值;若不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,曲线y=x2+mx–2与x轴交于A,B两点,点C的坐标为(0,1).当m变化时,解答下列问题:
(1)能否出现AC⊥BC的情况?说明理由;
(2)证明过A,B,C三点的圆在y轴上截得的弦长为定值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}满足:a1=1,an+1=
 an+
an+ 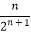
 (n∈N*).
(n∈N*).
(1)求最小的正实数M,使得对任意的n∈N* , 恒有0<an≤M.
(2)求证:对任意的n∈N* , 恒有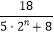 ≤an≤
≤an≤ 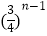 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 =lnx+ax2+(2a+1)x.
=lnx+ax2+(2a+1)x.(1)讨论
 的单调性;
的单调性;(2)当a﹤0时,证明
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】[选修4―4:坐标系与参数方程]
在直角坐标系xOy中,直线l1的参数方程为
 (t为参数),直线l2的参数方程为
(t为参数),直线l2的参数方程为 .设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
.设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.(1)写出C的普通方程;
(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设l3:ρ(cosθ+sinθ)
 =0,M为l3与C的交点,求M的极径.
=0,M为l3与C的交点,求M的极径.
相关试题

