【题目】在直角坐标系xOy中,曲线y=x2+mx–2与x轴交于A,B两点,点C的坐标为(0,1).当m变化时,解答下列问题:
(1)能否出现AC⊥BC的情况?说明理由;
(2)证明过A,B,C三点的圆在y轴上截得的弦长为定值.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)设![]() ,由AC⊥BC得
,由AC⊥BC得![]() ;由根与系数的关系得
;由根与系数的关系得![]() ,矛盾,所以不存在;(2)求出过A,B,C三点的圆的圆心坐标和半径,即可得圆的方程,再利用垂径定理求弦长.
,矛盾,所以不存在;(2)求出过A,B,C三点的圆的圆心坐标和半径,即可得圆的方程,再利用垂径定理求弦长.
试题解析:(1)不能出现AC⊥BC的情况,理由如下:
设![]() ,
, ![]() ,则
,则![]() 满足
满足![]() ,所以
,所以![]() .
.
又C的坐标为(0,1),故AC的斜率与BC的斜率之积为![]() ,所以不能出现AC⊥BC的情况.
,所以不能出现AC⊥BC的情况.
(2)BC的中点坐标为(![]() ),可得BC的中垂线方程为
),可得BC的中垂线方程为![]() .
.
由(1)可得![]() ,所以AB的中垂线方程为
,所以AB的中垂线方程为![]() .
.
联立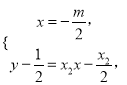 又
又![]() ,可得
,可得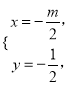
所以过A、B、C三点的圆的圆心坐标为(![]() ),半径
),半径![]()
故圆在y轴上截得的弦长为![]() ,即过A、B、C三点的圆在y轴上截得的弦长为定值.
,即过A、B、C三点的圆在y轴上截得的弦长为定值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从甲地到乙地要经过3个十字路口,设各路口信号灯工作相互独立,且在各路口遇到红灯的概率分别为
 .
.(Ⅰ)设
 表示一辆车从甲地到乙地遇到红灯的个数,求随机变量
表示一辆车从甲地到乙地遇到红灯的个数,求随机变量 的分布列和数学期望;
的分布列和数学期望;(Ⅱ)若有2辆车独立地从甲地到乙地,求这2辆车共遇到1个红灯的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三棱柱ABC﹣A1B1C1的侧面AA1C1C为正方形,侧面AA1B1B⊥侧面BB1C1C,且AC=2,AB=
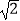 ,∠A1AB=45°,E、F分别为AA1、CC1的中点.
,∠A1AB=45°,E、F分别为AA1、CC1的中点. 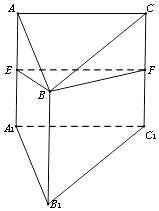
(1)求证:AA1⊥平面BEF;
(2)求二面角B﹣EB1﹣C1的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系xOy中,设椭圆E:
 =1(a>b>0),其中b=
=1(a>b>0),其中b=  a,F为椭圆的右焦点,P(1,1)为椭圆E内一点,PF⊥x轴.
a,F为椭圆的右焦点,P(1,1)为椭圆E内一点,PF⊥x轴. 
(1)求椭圆E的方程;
(2)过P点作斜率为k1 , k2的两条直线分别与椭圆交于点A,C和B,D.若满足|AP||PC|=|BP||DP|,问k1+k2是否为定值?若是,请求出此定值;若不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四面体ABCD中,△ABC是正三角形,AD=CD.

(1)证明:AC⊥BD;
(2)已知△ACD是直角三角形,AB=BD.若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}满足:a1=1,an+1=
 an+
an+ 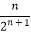
 (n∈N*).
(n∈N*).
(1)求最小的正实数M,使得对任意的n∈N* , 恒有0<an≤M.
(2)求证:对任意的n∈N* , 恒有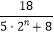 ≤an≤
≤an≤ 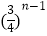 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 =lnx+ax2+(2a+1)x.
=lnx+ax2+(2a+1)x.(1)讨论
 的单调性;
的单调性;(2)当a﹤0时,证明
 .
.
相关试题

