【题目】设函数f(x)=3ax2﹣2(a+b)x+b,(0≤x≤1)其中a>0,b为任意常数.
(I)若b= ![]() ,f(x)=|x﹣
,f(x)=|x﹣ ![]() |在x∈[0,1]有两个不同的解,求实数a的范围.
|在x∈[0,1]有两个不同的解,求实数a的范围.
(II)当|f(0)|≤2,|f(1)|≤2时,求|f(x)|的最大值.
参考答案:
【答案】解:(I) ![]()
①当 ![]() 时,则
时,则 ![]() ,即3ax2﹣2ax=0,解得x=0
,即3ax2﹣2ax=0,解得x=0
②当 ![]() 时,则
时,则 ![]() ,即3ax2﹣2(a+1)x+1=0
,即3ax2﹣2(a+1)x+1=0
令t(x)=3ax2﹣2(a+1)x+1,因为 ![]() ,只要t(1)=a﹣1≥0即可
,只要t(1)=a﹣1≥0即可
所以a≥1
(II)设|f(x)|的最大值为M
①当 ![]() ,函数f(x)在[0,1]递减函数,M=|f(0)|≤2
,函数f(x)在[0,1]递减函数,M=|f(0)|≤2
②当 ![]() ,函数f(x)在[0,1]递增函数,M=|f(1)|≤2
,函数f(x)在[0,1]递增函数,M=|f(1)|≤2
③当 ![]() 时,即﹣a<b<2a时,
时,即﹣a<b<2a时, ![]()
(ⅰ)当 ![]() 时,即
时,即 ![]()
则 ![]() ,则f(1)﹣
,则f(1)﹣ ![]() =
= ![]() >0
>0
所以 M≤2
(ⅱ)当 ![]() 时,即
时,即 ![]() 时,可得
时,可得 ![]() ,即
,即 ![]()
则f(0)﹣ ![]()
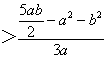 >0
>0
所以M≤2
综上M=2,当a=2,b=2,f(x)=12x2﹣12x+2,M=2
【解析】(Ⅰ)通过讨论x的范围,去掉绝对值,关于a的不等式,求出a的范围即可;(Ⅱ)求出函数的对称轴,通过讨论a的范围,确定函数的单调性,求出|f(x)|的最大值.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减.
上递减.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
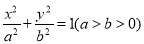 的左焦点为
的左焦点为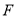 ,右顶点为
,右顶点为 ,离心率为
,离心率为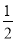 .已知
.已知 是抛物线
是抛物线 的焦点,
的焦点,  到抛物线的准线
到抛物线的准线 的距离为
的距离为 .
.(I)求椭圆的方程和抛物线的方程;
(II)设
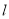 上两点
上两点 ,
,  关于
关于 轴对称,直线
轴对称,直线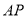 与椭圆相交于点
与椭圆相交于点 (
( 异于点
异于点 ),直线
),直线 与
与 轴相交于点
轴相交于点 .若
.若 的面积为
的面积为 ,求直线
,求直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,已知
 =
=  .
.
(1)求角C的大小;
(2)若c=2,求△ABC面积最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
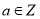 ,已知定义在R上的函数
,已知定义在R上的函数 在区间
在区间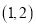 内有一个零点
内有一个零点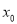 ,
, 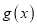 为
为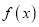 的导函数.
的导函数.(Ⅰ)求
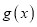 的单调区间;
的单调区间;(Ⅱ)设
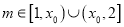 ,函数
,函数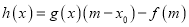 ,求证:
,求证:  ;
;(Ⅲ)求证:存在大于0的常数
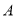 ,使得对于任意的正整数
,使得对于任意的正整数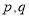 ,且
,且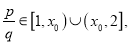 满足
满足 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】从甲地到乙地要经过3个十字路口,设各路口信号灯工作相互独立,且在各路口遇到红灯的概率分别为
 .
.(Ⅰ)设
 表示一辆车从甲地到乙地遇到红灯的个数,求随机变量
表示一辆车从甲地到乙地遇到红灯的个数,求随机变量 的分布列和数学期望;
的分布列和数学期望;(Ⅱ)若有2辆车独立地从甲地到乙地,求这2辆车共遇到1个红灯的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三棱柱ABC﹣A1B1C1的侧面AA1C1C为正方形,侧面AA1B1B⊥侧面BB1C1C,且AC=2,AB=
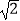 ,∠A1AB=45°,E、F分别为AA1、CC1的中点.
,∠A1AB=45°,E、F分别为AA1、CC1的中点. 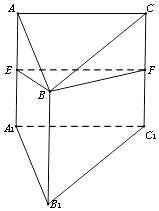
(1)求证:AA1⊥平面BEF;
(2)求二面角B﹣EB1﹣C1的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系xOy中,设椭圆E:
 =1(a>b>0),其中b=
=1(a>b>0),其中b=  a,F为椭圆的右焦点,P(1,1)为椭圆E内一点,PF⊥x轴.
a,F为椭圆的右焦点,P(1,1)为椭圆E内一点,PF⊥x轴. 
(1)求椭圆E的方程;
(2)过P点作斜率为k1 , k2的两条直线分别与椭圆交于点A,C和B,D.若满足|AP||PC|=|BP||DP|,问k1+k2是否为定值?若是,请求出此定值;若不是,请说明理由.
相关试题

