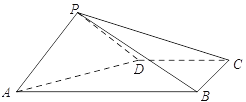
【题目】如图,在四棱锥![]() 中,平面
中,平面![]()
![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
参考答案:
【答案】(Ⅰ)见解析(Ⅱ)![]()
【解析】试题分析: ![]() 由直角及边长关系得
由直角及边长关系得![]() ,又因为平面
,又因为平面![]() 平面
平面![]() ,运用性质定理证得
,运用性质定理证得![]() 平面
平面![]() ,由判定定理证得
,由判定定理证得![]() 平面
平面![]()
![]() 建立空间直角坐标系,求法向量,计算可得。
建立空间直角坐标系,求法向量,计算可得。
解析:(Ⅰ)在底面![]() 中,
中, ![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,所以
,所以![]() ,
,
所以![]() ,
,
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() ,
,
又![]() 即
即![]() ,
,
又![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)分别延长![]() 和
和![]() 相交于一点
相交于一点![]() ,连结
,连结![]() ,则直线
,则直线![]() 即为所求直线
即为所求直线![]() ,
,
在平面![]() 内过
内过![]() 作
作![]() (如图),
(如图),
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,又
,又![]() ,
,
所以![]() 两两互相垂直.以
两两互相垂直.以![]() 为原点,向量
为原点,向量![]() 的方向分别为
的方向分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴的正方向建立空间直角坐标系
轴的正方向建立空间直角坐标系![]() (如图),另设
(如图),另设![]() ,
,
则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,

所以![]() ,
, ![]() ,
,
设![]() 是平面
是平面![]() 的法向量,
的法向量,
则![]() 即
即![]()
令![]() ,得
,得![]() .
.
显然![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
设二面角![]() 的大小为
的大小为![]() (
(![]() 为锐角).
为锐角).
所以![]() ,
,
所以二面角![]() 的的余弦值为
的的余弦值为![]() 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】若直角坐标平面内两点P,Q满足条件:①P,Q都在函数y=f(x)的图象上;②P,Q关于原点对称,则称(P,Q)是函数y=f(x)的一个“伙伴点组”(点组(P,Q)与(Q,P)看作同一个“伙伴点组”).已知函数f(x)=
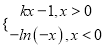 有两个“伙伴点组”,则实数k的取值范围是( )
有两个“伙伴点组”,则实数k的取值范围是( )A. (-∞,0) B. (0,1)
C.
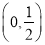 D. (0,+∞)
D. (0,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一张纸的长、宽分别为2
 a,2a,A,B,C,D分别是其四条边的中点,现将其沿图中虚线折起,使得P1,P2,P3,P4四点重合为一点P,从而得到一个多面体,关于该多面体的下列命题,正确的是________(写出所有正确命题的序号).
a,2a,A,B,C,D分别是其四条边的中点,现将其沿图中虚线折起,使得P1,P2,P3,P4四点重合为一点P,从而得到一个多面体,关于该多面体的下列命题,正确的是________(写出所有正确命题的序号).
①该多面体是三棱锥;②平面BAD⊥平面BCD;
③平面BAC⊥平面ACD;④该多面体外接球的表面积为5πa2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一张A4纸的长宽之比为
 ,
,  分别为
分别为 ,
,  的中点.现分别将△
的中点.现分别将△ ,△
,△ 沿
沿 ,
,  折起,且
折起,且 ,
,  在平面
在平面 同侧,下列命题正确的是__________.(写出所有正确命题的序号)
同侧,下列命题正确的是__________.(写出所有正确命题的序号)
①
 ,
,  ,
,  ,
,  四点共面;
四点共面;②当平面
 平面
平面 时,
时,  平面
平面 ;
;③当
 ,
,  重合于点
重合于点 时,平面
时,平面 平面
平面 ;
;④当
 ,
,  重合于点
重合于点 时,设平面
时,设平面 平面
平面
 ,则
,则 平面
平面 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数
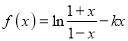 .
.(Ⅰ)讨论
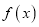 的单调性;
的单调性;(Ⅱ)当
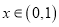 时,若
时,若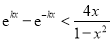 ,求实数
,求实数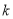 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(2018·日照一模)如图所示,ABCD-A1B1C1D1是长方体,O是B1D1的中点,直线A1C交平面AB1D1于点M,给出下列结论:

①A、M、O三点共线;②A、M、O、A1不共面;③A、M、C、O共面;④B、B1、O、M共面.
其中正确结论的序号为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正方体ABCD-A1B1C1D1中,E、F分别是AB和AA1的中点.

求证:(1)E、C、D1、F四点共面;
(2)CE、D1F、DA三线共点.
相关试题

