搜索
【题目】如图所示，正方体ABCD－A1B1C1D1中，E、F分别是AB和AA1的中点．
求证：(1)E、C、D1、F四点共面；
(2)CE、D1F、DA三线共点．
参考答案：
【答案】（1）见解析（2）见解析
【解析】试题分析：（1）要证四点共线，可证明EF//CD1，根据推论三可得四点共面；（2）从图中可以看出AD是平面ABCD与平面ADD1A1的交线，说明D1F与CE相交，则交点在两平面的交线上，从而得三线共点
试题解析：
证明：(1)如图所示，连接CD1、EF、A1B，
∵E、F分别是AB和AA1的中点，
∴FE∥A1B且EF＝
A1B.
∵A1D1∥BC，A1D1=BC
∴四边形A1BCD1是平行四边形，
∴A1B∥D1C，∴FE∥D1C，
∴EF与CD1可确定一个平面，即E、C、D1、F四点共面．
(2)由(1)知EF∥CD1，且EF＝CD1，
∴四边形CD1FE是梯形，
∴直线CE与D1F必相交，设交点为P，
则P∈CE平面ABCD，
且P∈D1F平面A1ADD1，
∴P∈平面ABCD且P∈平面A1ADD1.
又平面ABCD∩平面A1ADD1＝AD，
∴P∈AD，∴CE、D1F、DA三线共点．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四棱锥
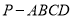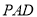
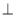中，平面
平面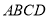
， 
， 
， 
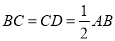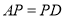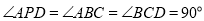．（Ⅰ）求证：
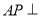平面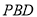
；（Ⅱ）求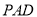平面
与平面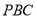
所成角的余弦值．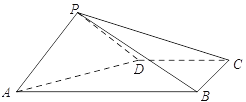
-
科目： 来源： 题型：
查看答案和解析>>【题目】函数
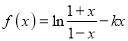.（Ⅰ）讨论
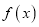的单调性；（Ⅱ）当
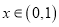时，若
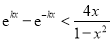，求实数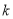
的取值范围. -
科目： 来源： 题型：
查看答案和解析>>【题目】(2018·日照一模)如图所示，ABCD－A1B1C1D1是长方体，O是B1D1的中点，直线A1C交平面AB1D1于点M，给出下列结论：
①A、M、O三点共线；②A、M、O、A1不共面；③A、M、C、O共面；④B、B1、O、M共面．
其中正确结论的序号为________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】关于函数图象的对称性与周期性，有下列说法：①若函数y＝f(x)满足f(x＋1)＝f(3＋x)，则f(x)的一个周期为T＝2；②若函数y＝f(x)满足f(x＋1)＝f(3－x)，则f(x)的图象关于直线x＝2对称；③函数y＝f(x＋1)与函数y＝f(3－x)的图象关于直线x＝2对称；④若函数
与函数f(x)的图象关于原点对称，则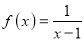
，其中正确的个数是()A. 1 B. 2
C. 3 D. 4
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知定义在R上的偶函数y＝f(x)满足：f(x＋4)＝f(x)＋f(2)，且当x∈[0,2]时，y＝f(x)单调递减，给出以下四个命题：
①f(2)＝0；②直线x＝－4为函数y＝f(x)图象的一条对称轴；③函数y＝f(x)在[8,10]上单调递增；④若关于x的方程f(x)＝m在[－6，－2]上的两根分别为x1，x2，则x1＋x2＝－8.
其中所有正确命题的序号为________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在数列{an}中，a1＝1，a2＝2，数列{anan＋1}是公比为q (q>0)的等比数列，则数列{an}的前2n项和S2n＝____________.
相关试题
