【题目】一装有水的直三棱柱![]() 容器(厚度忽略不计),上下底面均为边长为5的正三角形,侧棱为10,侧面
容器(厚度忽略不计),上下底面均为边长为5的正三角形,侧棱为10,侧面![]() 水平放置,如图所示,点
水平放置,如图所示,点![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别在棱
分别在棱![]() ,
, ![]() ,
, ![]() ,
, ![]() 上,水面恰好过点
上,水面恰好过点![]() ,
, ![]() ,
, ![]() ,
, ![]() ,且
,且![]() .
.

(1)证明: ![]() ;
;
(2)若底面![]() 水平放置时,求水面的高.
水平放置时,求水面的高.
参考答案:
【答案】(1)见解析(2) ![]()
【解析】试题分析:(1)直三棱柱容器侧面![]() 水平放置,所以平面
水平放置,所以平面![]() 平面
平面![]() ,由面面平行性质得
,由面面平行性质得![]() .(2)当底面ABC水平放置时,水的形状为四棱柱形,由已知条件求出水的体积,由于是三棱柱形容器,故水的体积可以用三角形的面积直接表示出,不必求三角形的面积.
.(2)当底面ABC水平放置时,水的形状为四棱柱形,由已知条件求出水的体积,由于是三棱柱形容器,故水的体积可以用三角形的面积直接表示出,不必求三角形的面积.
(1)证明:因为直三棱柱容器侧面![]() 水平放置,
水平放置,
所以平面![]() 平面
平面![]() ,
,
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() .
.
(2)解;当侧面![]() 水平放置时,可知液体部分是直四棱柱,
水平放置时,可知液体部分是直四棱柱,
其高即为直三棱柱![]() 容器的高,即侧棱长10.
容器的高,即侧棱长10.
由(I)可得![]() ,又
,又![]() ,
,
所以![]() .
.
当底面![]() 水平放置时,设水面的高为
水平放置时,设水面的高为![]() ,由于两种状态下水的体积相等,
,由于两种状态下水的体积相等,
所以![]() ,即
,即![]() ,
,
解得![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
 ,圆
,圆 ,点
,点 是圆上一动点,
是圆上一动点,  的垂直平分线与
的垂直平分线与 交于点
交于点 .
.(1)求点
 的轨迹方程;
的轨迹方程;(2)设点
 的轨迹为曲线
的轨迹为曲线 ,过点
,过点 且斜率不为0的直线
且斜率不为0的直线 与
与 交于
交于 两点,点
两点,点 关于
关于 轴的对称点为
轴的对称点为 ,证明直线
,证明直线 过定点,并求
过定点,并求 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
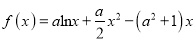 .
.(1)讨论函数
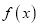 的单调性;
的单调性;(2)当
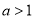 时,记函数
时,记函数 的极小值为
的极小值为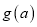 ,若
,若 恒成立,求满足条件的最小整数
恒成立,求满足条件的最小整数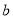 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
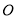 为坐标原点,椭圆
为坐标原点,椭圆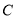 :
:  的左焦点是
的左焦点是 ,离心率为
,离心率为 ,且
,且 上任意一点
上任意一点 到
到 的最短距离为
的最短距离为 .
.(1)求
 的方程;
的方程;(2)过点
 的直线
的直线 (不过原点)与
(不过原点)与 交于两点
交于两点 、
、 ,
,  为线段
为线段 的中点.
的中点.(i)证明:直线
 与
与 的斜率乘积为定值;
的斜率乘积为定值;(ii)求
 面积的最大值及此时
面积的最大值及此时 的斜率.
的斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知四棱锥
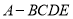 中,底面
中,底面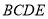 为直角梯形,
为直角梯形, 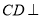 平面
平面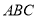 ,侧面
,侧面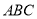 是等腰直角三角形,
是等腰直角三角形, 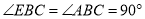 ,
, 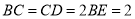 ,点
,点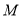 是棱
是棱 的中点.
的中点.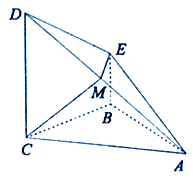
(1)证明:平面
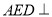 平面
平面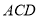 ;
;(2)求锐二面角
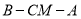 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 被直线
被直线 ,
,  分成面积相等的四个部分,且截
分成面积相等的四个部分,且截 轴所得线段的长为2.
轴所得线段的长为2. (1)求
 的方程;
的方程;(2)若存在过点
 的直线与
的直线与 相交于
相交于 ,
,  两点,且点
两点,且点 恰好是线段
恰好是线段 的中点,求实数
的中点,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
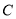 :
:  的焦点为
的焦点为 ,准线为
,准线为 ,三个点
,三个点 ,
,  ,
,  中恰有两个点在
中恰有两个点在 上.
上.(1)求抛物线
 的标准方程;
的标准方程;(2)过
 的直线交
的直线交 于
于 ,
,  两点,点
两点,点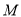 为
为 上任意一点,证明:直线
上任意一点,证明:直线 ,
,  ,
,  的斜率成等差数列.
的斜率成等差数列.
相关试题

