【题目】已知四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形, ![]() 平面
平面![]() ,侧面
,侧面![]() 是等腰直角三角形,
是等腰直角三角形, ![]() ,
, ![]() ,点
,点![]() 是棱
是棱![]() 的中点.
的中点.
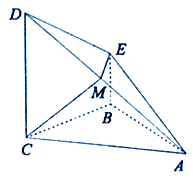
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求锐二面角![]() 的余弦值.
的余弦值.
参考答案:
【答案】(1)见解析(2) ![]()
【解析】,
试题分析:(1)取AC的中点F,连接BF,可证![]() 平面ACD,又可证四边形BFME是平行四边形.可得 EM//BF,可证
平面ACD,又可证四边形BFME是平行四边形.可得 EM//BF,可证![]() 平面ACD,从而平面
平面ACD,从而平面![]() 平面
平面![]() ;(2)利用空间直角坐标进行向量运算,根据法向量夹角即可求出.
;(2)利用空间直角坐标进行向量运算,根据法向量夹角即可求出.
试题解析:
(1)证明:取AC的中点F,连接BF,
因为AB=BC,所以![]() ,
, ![]() 平面ABC,所以CD
平面ABC,所以CD ![]() .
.
又![]() 所以
所以![]() 平面ACD.①
平面ACD.①
因为AM=MD,AF=CF,所以![]() .
.
因为![]()
![]() ,所以
,所以![]() //MF,
//MF,
所以四边形BFME是平行四边形.所以EM//BF.②
由①②,得![]() 平面ACD,所以平面
平面ACD,所以平面![]() 平面
平面![]() ;
;
(2)解: ![]() BE
BE![]() 平面ABC,
平面ABC,
![]() 又
又![]() ,
,
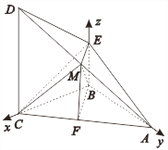
![]() 以点B为原点,直线BC、BA、BE分别为x,y,z轴,
以点B为原点,直线BC、BA、BE分别为x,y,z轴,
建立空间直角坐标系B-xyz.
由![]() ,得B(0,0,0),C(2,0,0),A(0,2,0),D(2,0,2).
,得B(0,0,0),C(2,0,0),A(0,2,0),D(2,0,2).
由中点坐标公式得![]() ,
, ![]() ,
,![]() ,
,
设向量![]() 为平面BMC的一个法向量,则
为平面BMC的一个法向量,则![]() 即
即![]()
令y=1,得x=0,z=-1,即![]() ,
,
由(I)知, ![]() 是平面ACD的一个法向量.
是平面ACD的一个法向量.
设二面角B-CM-A的平面角为![]() ,
,
则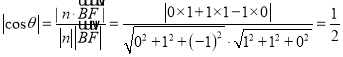 ,
,
又二面角B-CM-A为锐二面角,故![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
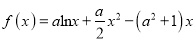 .
.(1)讨论函数
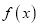 的单调性;
的单调性;(2)当
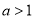 时,记函数
时,记函数 的极小值为
的极小值为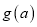 ,若
,若 恒成立,求满足条件的最小整数
恒成立,求满足条件的最小整数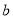 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 为坐标原点,椭圆
为坐标原点,椭圆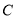 :
:  的左焦点是
的左焦点是 ,离心率为
,离心率为 ,且
,且 上任意一点
上任意一点 到
到 的最短距离为
的最短距离为 .
.(1)求
 的方程;
的方程;(2)过点
 的直线
的直线 (不过原点)与
(不过原点)与 交于两点
交于两点 、
、 ,
,  为线段
为线段 的中点.
的中点.(i)证明:直线
 与
与 的斜率乘积为定值;
的斜率乘积为定值;(ii)求
 面积的最大值及此时
面积的最大值及此时 的斜率.
的斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】一装有水的直三棱柱
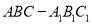 容器(厚度忽略不计),上下底面均为边长为5的正三角形,侧棱为10,侧面
容器(厚度忽略不计),上下底面均为边长为5的正三角形,侧棱为10,侧面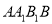 水平放置,如图所示,点
水平放置,如图所示,点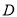 ,
, 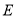 ,
, 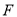 ,
, 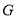 分别在棱
分别在棱 ,
,  ,
, 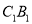 ,
, 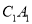 上,水面恰好过点
上,水面恰好过点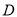 ,
, 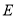 ,
, 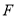 ,
, 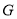 ,且
,且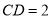 .
.
(1)证明:
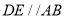 ;
;(2)若底面
 水平放置时,求水面的高.
水平放置时,求水面的高. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 被直线
被直线 ,
,  分成面积相等的四个部分,且截
分成面积相等的四个部分,且截 轴所得线段的长为2.
轴所得线段的长为2. (1)求
 的方程;
的方程;(2)若存在过点
 的直线与
的直线与 相交于
相交于 ,
,  两点,且点
两点,且点 恰好是线段
恰好是线段 的中点,求实数
的中点,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 :
:  的焦点为
的焦点为 ,准线为
,准线为 ,三个点
,三个点 ,
,  ,
,  中恰有两个点在
中恰有两个点在 上.
上.(1)求抛物线
 的标准方程;
的标准方程;(2)过
 的直线交
的直线交 于
于 ,
,  两点,点
两点,点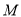 为
为 上任意一点,证明:直线
上任意一点,证明:直线 ,
,  ,
,  的斜率成等差数列.
的斜率成等差数列. -
科目: 来源: 题型:
查看答案和解析>>【题目】某P2P平台需要了解该平台投资者的大致年龄分布,发现其投资者年龄大多集中在区间[20,50]岁之间,对区间[20,50]岁的人群随机抽取20人进行了一次理财习惯调查,得到如下统计表和各年龄段人数频率分布直方图:
组数
分组
人数(单位:人)
第一组
[20,25)
2
第二组
[25,30)
a
第三组
[30,35)
5
第四组
[35,40)
4
第五组
[40,45)
3
第六组
[45,50]
2

(Ⅰ)求a的值并画出频率分布直方图;
(Ⅱ)在统计表的第五与第六组的5人中,随机选取2人,求这2人的年龄都小于45岁的概率.
相关试题

