【题目】在直角坐标系![]() 中,点
中,点![]() 到两点
到两点![]() ,
,![]() 的距离之和等于4,设点
的距离之和等于4,设点![]() 的轨迹为
的轨迹为![]() ,直线
,直线![]() 与
与![]() 交于
交于![]() 两点,
两点,
(1)写出![]() 的方程;
的方程;
(2)若![]() ,求
,求![]() 的值.
的值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)由题中条件:“点![]() 到两点
到两点![]() ,
,![]() 的距离之和等于
的距离之和等于![]() ,”结合椭圆的定义知其轨迹式样,从而求得其方程;(2)先将直线方程与椭圆方程联立方程组,消去
,”结合椭圆的定义知其轨迹式样,从而求得其方程;(2)先将直线方程与椭圆方程联立方程组,消去![]() 得到一个一元二次方程,再利用根与系数的关系结合向量垂直的条件列关于
得到一个一元二次方程,再利用根与系数的关系结合向量垂直的条件列关于![]() 方程式即可求得参数
方程式即可求得参数![]() 值.
值.
试题解析:(1)设P(x,y),由椭圆定义可知,点P的轨迹C是以(0,-![]() )、(0,
)、(0,![]() )为焦点,长半轴为2的椭圆,它的短半轴
)为焦点,长半轴为2的椭圆,它的短半轴![]() ,
,
故曲线C的方程为![]() .
.
(2)设A(x1,y1),B(x2,y2),
联立方程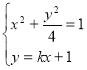
消去y并整理得(k2+4)x2+2kx-3=0.
其中Δ=4k2+12(k2+4)>0恒成立.
故![]()
![]() ,
,![]() .
.
若![]() ,即x1x2+y1y2=0.
,即x1x2+y1y2=0.
而y1y2=k2x1x2+k(x1+x2)+1,
于是x1x2+y1y2=-![]()
![]() ,
,
化简得-4k2+1=0,所以k=±![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为贯彻落实教育部等6部门《关于加快发展青少年校园足球的实施意见》,全面提高我市中学生的体质健康水平,普及足球知识和技能,市教体局决定矩形春季校园足球联赛,为迎接此次联赛,甲同学选拔了20名学生组成集训队,现统计了这20名学生的身高,记录如下表:
身高(
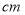 )
)168
174
175
176
178
182
185
188
人数
1
2
4
3
5
1
3
1
(1)请计算这20名学生的身高中位数、众数,并补充完成下面的茎叶图;

(2)身高为185
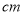 和188
和188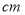 的四名学生分别为
的四名学生分别为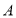 ,
,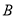 ,
,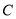 ,
,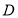 ,先从这四名学生中选2名担任正副门将,请利用列举法列出所有可能情况,并求学生
,先从这四名学生中选2名担任正副门将,请利用列举法列出所有可能情况,并求学生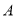 入选正门将的概率.
入选正门将的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
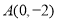 ,椭圆
,椭圆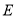 :
: 的离心率为
的离心率为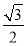 ,
,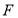 是椭圆
是椭圆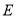 的右焦点,直线
的右焦点,直线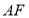 的斜率为
的斜率为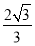 ,
, 为坐标原点.
为坐标原点.(1)求
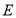 的方程;
的方程;(2)设过点
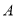 的动直线
的动直线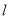 与
与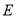 相交于
相交于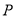 ,
,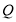 两点,当
两点,当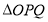 的面积最大时,求
的面积最大时,求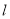 的直线方程.
的直线方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的圆台中,
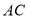 是下底面圆
是下底面圆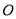 的直径,
的直径,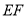 是上底面圆
是上底面圆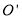 的直径,
的直径, 是圆台的一条母线.
是圆台的一条母线.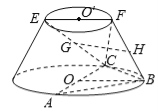
(1)已知
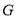 ,
,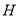 分别为
分别为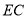 ,
,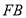 的中点,求证:
的中点,求证: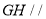 平面
平面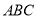 ;
;(2)已知
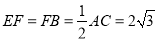 ,
,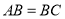 ,求二面角
,求二面角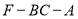 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在数列
 中,
中, ,
, ,
,(1)设
 ,证明:数列
,证明:数列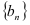 是等差数列;
是等差数列;(2)求数列
 的前
的前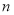 项和.
项和. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 为等差数列,且
为等差数列,且 ,
, .
.(1)求
 的通项公式;
的通项公式;(2)若等比数列
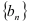 满足
满足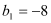 ,
,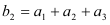 ,求
,求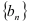 的前
的前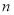 项和公式.
项和公式. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;②设有一个回归方程
 ,变量
,变量 增加一个单位时,
增加一个单位时, 平均增加5个单位;③线性回归方程
平均增加5个单位;③线性回归方程 必过
必过 ;④在吸烟与患肺病这两个分类变量的计算中,从独立性检验知,有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患肺病;其中错误的个数是( )
;④在吸烟与患肺病这两个分类变量的计算中,从独立性检验知,有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患肺病;其中错误的个数是( )A.0 B.1 C. 2 D.3
相关试题

