【题目】在四棱锥![]() 中,底面
中,底面![]() 为正方形,
为正方形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点.
的中点.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求三棱锥![]() 的体积;
的体积;
(Ⅲ)求证:平面![]() 平面
平面![]() .
.
参考答案:
【答案】(Ⅰ)详见解析(Ⅱ)![]() (Ⅲ)详见解析
(Ⅲ)详见解析
【解析】试题分析:
(Ⅰ)证明:连接![]() ,与
,与![]() 交于点
交于点![]() ,连接
,连接![]() ,易证
,易证![]() ,可知
,可知![]() 平面
平面![]() .
.
(Ⅱ)由题可求 ![]() ,进而证明
,进而证明![]() .,则三棱锥
.,则三棱锥![]() 的体积可求;
的体积可求;
(Ⅲ)首先证明![]() 平面
平面![]() ,又
,又![]() ,即
,即![]() 平面
平面![]() ,,所以平面
,,所以平面![]() 平面
平面![]() .
.
试题解析:(Ⅰ)证明:连接![]() ,与
,与![]() 交于点
交于点![]() ,连接
,连接![]() ,
,
在![]() 中,
中, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点,
的中点,
所以![]() ,
,
又因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)解:因为![]() 平面
平面![]() ,所以
,所以![]() 为棱锥
为棱锥![]() 的高.
的高.
因为![]() ,底面
,底面![]() 是正方形,
是正方形,
所以![]()
![]() ,
,
因为![]() 为
为![]() 中点,所以
中点,所以![]() ,
,
所以![]() .
.
(Ⅲ)证明:因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() ,
,
在等腰直角![]() 中,
中, ![]() ,
,
又![]() ,
, ![]()
![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
又![]() ,
,
所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 :
:  经过椭圆
经过椭圆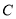 :
:  的左右焦点
的左右焦点 ,且与椭圆
,且与椭圆 在第一象限的交点为
在第一象限的交点为 ,且
,且 三点共线,直线
三点共线,直线 交椭圆
交椭圆 于
于 ,
,  两点,且
两点,且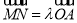 (
( ).
).(1)求椭圆
 的方程;
的方程; (2)当三角形
 的面积取得最大值时,求直线
的面积取得最大值时,求直线 的方程.
的方程.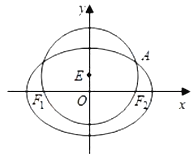
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是某市环保局连续30天对空气质量指数的监测数据:
61 76 70 56 81 91 55 91 75 81
88 67 101 103 57 91 77 86 81 83
82 82 64 79 86 85 75 71 49 45
(Ⅰ)完成下面的频率分布表;
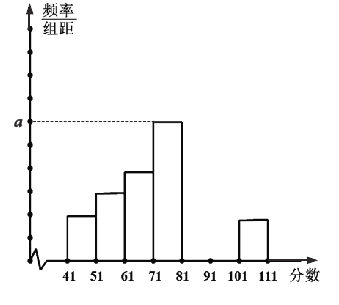
(Ⅱ)完成下面的频率分布直方图,并写出频率分布直方图中
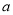 的值;
的值;(Ⅲ)在本月空气质量指数大于等于91的这些天中随机选取两天,求这两天中至少有一天空气质量指数在区间
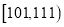 内的概率.
内的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行调查,得到的统计数据如下表所示:
积极参加班级工作
不积极参加班级工作
合计
学习积极性高
18
7
25
学习积极性不高
6
19
25
合计
24
26
50
(1)如果随机调查这个班的一名学生,那么抽到不积极参加班级工作且学习积极性不高的学生的概率是多少?
(2)若不积极参加班级工作且学习积极性高的7名学生中有两名男生,现从中抽取两名学生参加某项活动,问两名学生中有1名男生的概率是多少?
(3)学生的学习积极性与对待班极工作的态度是否有关系?请说明理由.
附:

0.10
0.05
0.025
0.010
0.005
0.001
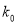
2.706
3.841
5.024
6.635
7.879
10.828
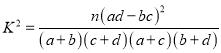
-
科目: 来源: 题型:
查看答案和解析>>【题目】在实数
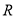 中定义一种新运算:
中定义一种新运算:  ,对实数
,对实数 经过运算
经过运算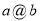 后是一个确定的唯一的实数。
后是一个确定的唯一的实数。 运算有如下性质:(1)对任意实数
运算有如下性质:(1)对任意实数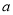 ,
, 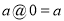 ;(2)对任意实数
;(2)对任意实数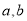 ,
, 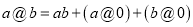 那么:关于函数
那么:关于函数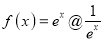 的性质下列说法正确的是:①函数
的性质下列说法正确的是:①函数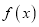 的最小值为3;②函数
的最小值为3;②函数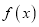 是偶函数;③函数
是偶函数;③函数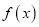 在
在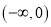 上为减函数,这三种说法正确的有__________.
上为减函数,这三种说法正确的有__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(Ⅰ)求函数
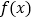 的单调递增区间;
的单调递增区间;(Ⅱ)用反证法证明:在
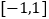 上,不存在不同的两点
上,不存在不同的两点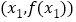 ,
,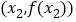 ,使得
,使得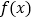 的图象在这两点处的切线相互平行.
的图象在这两点处的切线相互平行. -
科目: 来源: 题型:
查看答案和解析>>【题目】经测算,某型号汽车在匀速行驶过程中每小时耗油量
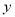 (升)与速度
(升)与速度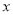 (千米/每小时)
(千米/每小时) 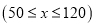 的关系可近似表示为:
的关系可近似表示为: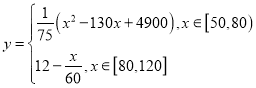 .
.(Ⅰ)该型号汽车速度为多少时,可使得每小时耗油量最低?
(Ⅱ)已知
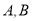 两地相距120公里,假定该型号汽车匀速从
两地相距120公里,假定该型号汽车匀速从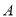 地驶向
地驶向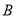 地,则汽车速度为多少时总耗油量最少?
地,则汽车速度为多少时总耗油量最少?
相关试题

