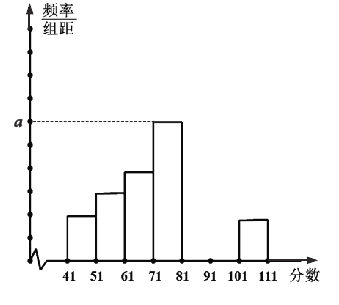
【题目】下面是某市环保局连续30天对空气质量指数的监测数据:
61 76 70 56 81 91 55 91 75 81
88 67 101 103 57 91 77 86 81 83
82 82 64 79 86 85 75 71 49 45
(Ⅰ)完成下面的频率分布表;
(Ⅱ)完成下面的频率分布直方图,并写出频率分布直方图中![]() 的值;
的值;
(Ⅲ)在本月空气质量指数大于等于91的这些天中随机选取两天,求这两天中至少有一天空气质量指数在区间![]() 内的概率.
内的概率.

参考答案:
【答案】(Ⅰ)答案见解析;(Ⅱ)答案见解析;(Ⅲ)0.7.
【解析】试题分析:
(1)由题意计算相应的频数和频率即可补全频率分布表;
(2)完成频率分布直方图,结合区间![]() 的频率为
的频率为![]() ,可得
,可得![]() ;
;
(3)由题意列出所有可能的事件,然后结合题意和古典概型的计算公式可得这两天中至少有一天空气质量指数在区间![]() 内的概率是0.7.
内的概率是0.7.
试题解析:
(Ⅰ)如下图所示
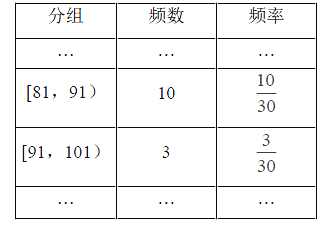
(Ⅱ)如下图所示
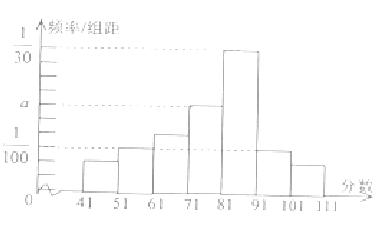
由已知,空气质量指数在区间![]() 的频率为
的频率为![]() ,所以
,所以![]()
(Ⅲ)设![]() 表示事件“在本月空气质量指数大于等于91的这些天中随机选取两天,这两天中至少有一天空气质量指数在区间
表示事件“在本月空气质量指数大于等于91的这些天中随机选取两天,这两天中至少有一天空气质量指数在区间![]() 内”,
内”,
由己知,质量指数在区间![]() 内的有3天,
内的有3天,
记这三天分别为![]() ,
,
质量指数在区间![]() 内的有2天,
内的有2天,
记这两天分别为![]() ,
,
则选取的所有可能结果为: ![]()
基本事件数为10.
事件“至少有一天空气质量指数在区间![]() 内”的可能结果为:
内”的可能结果为: ![]()
基本事件数为 7,
所以![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下茎叶图记录了甲,乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以
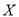 表示.
表示.
(1)如果
 ,求乙组同学植树棵数的平均数和方差;
,求乙组同学植树棵数的平均数和方差;(2)如果
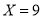 ,分别从甲,乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率.(注:方差
,分别从甲,乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率.(注:方差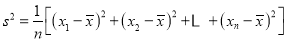 ,其中
,其中 为
为 ,
, 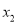 ,……,
,……,  的平均数)
的平均数) -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校用“10分制”调查本校学生对教师教学的满意度,现从学生中随机抽取16名,以下茎叶图记录了他们对该校教师教学满意度的分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):
(Ⅰ)若教学满意度不低于9.5分,则称该生对教师的教学满意度为“极满意”.求从这16人中随机选取3人,至少有1人是“极满意”的概率;
(Ⅱ)以这16人的样本数据来估计整个学校的总体数据,若从该校所有学生中(学生人数很多)任选3人,记
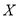 表示抽到“极满意”的人数,求
表示抽到“极满意”的人数,求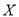 的分布列及数学期望.
的分布列及数学期望.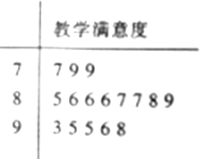
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 :
:  经过椭圆
经过椭圆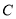 :
:  的左右焦点
的左右焦点 ,且与椭圆
,且与椭圆 在第一象限的交点为
在第一象限的交点为 ,且
,且 三点共线,直线
三点共线,直线 交椭圆
交椭圆 于
于 ,
,  两点,且
两点,且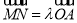 (
( ).
).(1)求椭圆
 的方程;
的方程; (2)当三角形
 的面积取得最大值时,求直线
的面积取得最大值时,求直线 的方程.
的方程.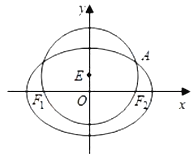
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行调查,得到的统计数据如下表所示:
积极参加班级工作
不积极参加班级工作
合计
学习积极性高
18
7
25
学习积极性不高
6
19
25
合计
24
26
50
(1)如果随机调查这个班的一名学生,那么抽到不积极参加班级工作且学习积极性不高的学生的概率是多少?
(2)若不积极参加班级工作且学习积极性高的7名学生中有两名男生,现从中抽取两名学生参加某项活动,问两名学生中有1名男生的概率是多少?
(3)学生的学习积极性与对待班极工作的态度是否有关系?请说明理由.
附:

0.10
0.05
0.025
0.010
0.005
0.001
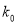
2.706
3.841
5.024
6.635
7.879
10.828
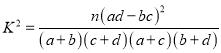
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥
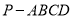 中,底面
中,底面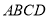 为正方形,
为正方形, 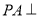 平面
平面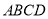 ,
, 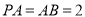 ,
, 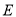 ,
, 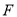 分别是
分别是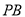 ,
, 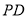 的中点.
的中点. 
(Ⅰ)求证:
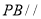 平面
平面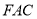 ;
;(Ⅱ)求三棱锥
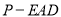 的体积;
的体积;(Ⅲ)求证:平面
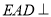 平面
平面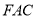 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在实数
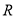 中定义一种新运算:
中定义一种新运算:  ,对实数
,对实数 经过运算
经过运算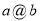 后是一个确定的唯一的实数。
后是一个确定的唯一的实数。 运算有如下性质:(1)对任意实数
运算有如下性质:(1)对任意实数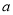 ,
, 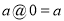 ;(2)对任意实数
;(2)对任意实数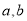 ,
, 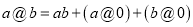 那么:关于函数
那么:关于函数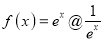 的性质下列说法正确的是:①函数
的性质下列说法正确的是:①函数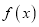 的最小值为3;②函数
的最小值为3;②函数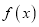 是偶函数;③函数
是偶函数;③函数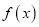 在
在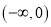 上为减函数,这三种说法正确的有__________.
上为减函数,这三种说法正确的有__________.
相关试题

