【题目】已知圆C:(x﹣3)2+(y﹣4)2=4,直线l过定点A(1,0).
(1)若l与圆C相切,求l的方程;
(2)若l与圆C相交于P、Q两点,若|PQ|=2 ![]() ,求此时直线l的方程.
,求此时直线l的方程.
参考答案:
【答案】
(1)解:若直线l的斜率不存在,则直线l:x=1,符合题意.
若直线l斜率存在,设直线l的方程为y=k(x﹣1),即kx﹣y﹣k=0.
由题意知,圆心(3,4)到已知直线l的距离等于半径2,即: ![]() =2,解之得k=
=2,解之得k= ![]() ,
,
此时直线的方程为3x﹣4y﹣3=0.
综上可得,所求直线l的方程是x=1或3x﹣4y﹣3=0
(2)解:直线与圆相交,斜率必定存在,且不为0,设直线方程为kx﹣y﹣k=0,
因为|PQ|=2 ![]() =2
=2 ![]() =2
=2 ![]() ,求得弦心距d=
,求得弦心距d= ![]() ,
,
即 ![]() =
= ![]() ,求得 k=1或k=7,
,求得 k=1或k=7,
所求直线l方程为x﹣y﹣1=0或7x﹣y﹣7=0
【解析】(1)分直线的斜率存在和不存在两种情况,分别根据直线和圆相切的性质求得直线的方程,综合可得结论.(2)用点斜式设出直线的方程,利用条件以及点到直线的距离公式,弦长公式求出斜率的值,可得直线的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知动点P(x,y)满足方程xy=1(x>0).
(Ⅰ)求动点P到直线l:x+2y﹣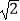 =0距离的最小值;
=0距离的最小值;
(Ⅱ)设定点A(a,a),若点P,A之间的最短距离为2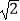 ,求满足条件的实数a的取值.
,求满足条件的实数a的取值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 cosx(sinx+cosx). (Ⅰ)若0<α<
cosx(sinx+cosx). (Ⅰ)若0<α<  ,且sinα=
,且sinα=  ,求f(α)的值;
,求f(α)的值;
(Ⅱ)求函数f(x)的最小正周期及单调递增区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=
 (Ⅰ)当
(Ⅰ)当 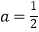 时,求函数f(x)的值域;
时,求函数f(x)的值域;
(Ⅱ)若函数f(x)是(﹣∞,+∞)上的减函数,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知点A(1,0),D(﹣1,0),点B,C在单位圆O上,且∠BOC=
 .
. 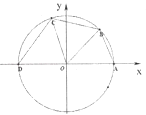
(Ⅰ)若点B(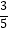 ,
, 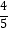 ),求cos∠AOC的值;
),求cos∠AOC的值;
(Ⅱ)设∠AOB=x(0<x<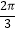 ),四边形ABCD的周长为y,将y表示成x的函数,并求出y的最大值.
),四边形ABCD的周长为y,将y表示成x的函数,并求出y的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的几何体中,四边形ABCD是平行四边形,∠ABD=90°,EB⊥平面ABCD,EF∥AB,AB=2,EB=
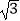 ,EF=1,BC=
,EF=1,BC= 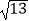 ,且M是BD的中点..
,且M是BD的中点.. 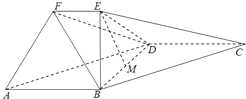
(1)求证:EM∥平面ADF;
(2)求直线DF和平面ABCD所成角的正切值;
(3)求二面角D﹣AF﹣B的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)是定义在[﹣1,1]上的奇函数,且f(1)=1,若x,y∈[﹣1,1],x+y≠0有(x+y)[f(x)+f(y)]>0.
(1)判断f(x)的单调性,并加以证明;
(2)解不等式 ;
;
(3)若f(x)≤m2﹣2am+1对所有x∈[﹣1,1],a∈[﹣1,1]恒成立.求实数m的取值范围.
相关试题

