【题目】已知函数f(x)= ![]() cosx(sinx+cosx). (Ⅰ)若0<α<
cosx(sinx+cosx). (Ⅰ)若0<α< ![]() ,且sinα=
,且sinα= ![]() ,求f(α)的值;
,求f(α)的值;
(Ⅱ)求函数f(x)的最小正周期及单调递增区间.
参考答案:
【答案】解:(Ⅰ)∵0<α< ![]() ,且sinα=
,且sinα= ![]() , ∴cosα=
, ∴cosα= ![]() ,
,
∴f(α)= ![]() cosα(sinα+cosα)
cosα(sinα+cosα)
= ![]() ×
× ![]() ×(
×( ![]() +
+ ![]() )
)
= ![]() ;
;
(Ⅱ)函数f(x)= ![]() cosx(sinx+cosx)
cosx(sinx+cosx)
= ![]() (cosxsinx+cos2x)
(cosxsinx+cos2x)
= ![]() sin2x+
sin2x+ ![]() cos2x+
cos2x+ ![]()
=sin(2x+ ![]() )+
)+ ![]() ,
,
∴f(x)的最小正周期为π;
令﹣ ![]() +2kπ≤2x+
+2kπ≤2x+ ![]() ≤
≤ ![]() +2kπ,k∈Z,
+2kπ,k∈Z,
解得﹣ ![]() +kπ≤x≤
+kπ≤x≤ ![]() +kπ,k∈Z,
+kπ,k∈Z,
∴函数f(x)的单调减区间为[﹣ ![]() +kπ,
+kπ, ![]() +kπ],k∈Z
+kπ],k∈Z
【解析】(Ⅰ)根据同角的三角函数关系,求出sinα、cosα的值,再计算f(α)的值;(Ⅱ)化函数f(x)为正弦型函数,即可求出f(x)的最小正周期和单调减区间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AD⊥AB,DC∥AB,PA=1,AB=2,PD=BC=
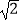 .
. 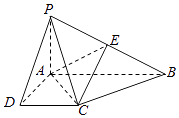
(1)求证:平面PAD⊥平面PCD;
(2)试在棱PB上确定一点E,使截面AEC把该几何体分成的两部分PDCEA与EACB的体积比为2:1;
(3)在(2)的条件下,求二面角E﹣AC﹣P的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P—ABCD中,平面PAD⊥底面ABCD,其中底面ABCD为等腰梯形,AD∥BC,PA=AB=BC=CD=2,PD=2
 ,PA⊥PD,Q为PD的中点.
,PA⊥PD,Q为PD的中点.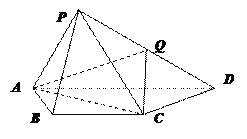
(Ⅰ)证明:CQ∥平面PAB;
(Ⅱ)求直线PD与平面AQC所成角的正弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知动点P(x,y)满足方程xy=1(x>0).
(Ⅰ)求动点P到直线l:x+2y﹣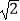 =0距离的最小值;
=0距离的最小值;
(Ⅱ)设定点A(a,a),若点P,A之间的最短距离为2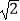 ,求满足条件的实数a的取值.
,求满足条件的实数a的取值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=
 (Ⅰ)当
(Ⅰ)当 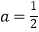 时,求函数f(x)的值域;
时,求函数f(x)的值域;
(Ⅱ)若函数f(x)是(﹣∞,+∞)上的减函数,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C:(x﹣3)2+(y﹣4)2=4,直线l过定点A(1,0).
(1)若l与圆C相切,求l的方程;
(2)若l与圆C相交于P、Q两点,若|PQ|=2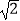 ,求此时直线l的方程.
,求此时直线l的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知点A(1,0),D(﹣1,0),点B,C在单位圆O上,且∠BOC=
 .
. 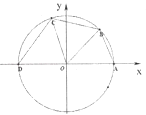
(Ⅰ)若点B(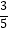 ,
, 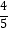 ),求cos∠AOC的值;
),求cos∠AOC的值;
(Ⅱ)设∠AOB=x(0<x<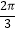 ),四边形ABCD的周长为y,将y表示成x的函数,并求出y的最大值.
),四边形ABCD的周长为y,将y表示成x的函数,并求出y的最大值.
相关试题

