【题目】设函数f(x)= ![]() (Ⅰ)当
(Ⅰ)当 ![]() 时,求函数f(x)的值域;
时,求函数f(x)的值域;
(Ⅱ)若函数f(x)是(﹣∞,+∞)上的减函数,求实数a的取值范围.
参考答案:
【答案】解:(Ⅰ)a= ![]() 时,f(x)=
时,f(x)= 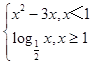 , 当x<1时,f(x)=x2﹣3x是减函数,所以f(x)>f(1)=﹣2,即x<1时,f(x)的值域是(﹣2,+∞).
, 当x<1时,f(x)=x2﹣3x是减函数,所以f(x)>f(1)=﹣2,即x<1时,f(x)的值域是(﹣2,+∞).
当x≥1时,f(x)= ![]() 是减函数,所以f(x)≤f(1)=0,即x≥1时,f(x)的值域是(﹣∞,0].
是减函数,所以f(x)≤f(1)=0,即x≥1时,f(x)的值域是(﹣∞,0].
于是函数f(x)的值域是(﹣∞,0]∪(﹣2,+∞)=R.
(Ⅱ)若函数f(x)是(﹣∞,+∞)上的减函数,则下列①②③三个条件同时成立:
①当x<1,f(x)=x2﹣(4a+1)x﹣8a+4是减函数,于是 ![]() ≥1,则a≥
≥1,则a≥ ![]() .
.
②x≥1时,f(x)= ![]() 是减函数,则0<a<1.
是减函数,则0<a<1.
③12﹣(4a+1)1﹣8a+4≥0,则a≤ ![]() .
.
于是实数a的取值范围是[ ![]() ,
, ![]() ]
]
【解析】(Ⅰ)a= ![]() 时,f(x)=
时,f(x)= 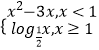 ,当x<1时,f(x)=x2﹣3x是减函数,可求此时函数f(x)的值域;同理可求得当x≥1时,减函数f(x)=
,当x<1时,f(x)=x2﹣3x是减函数,可求此时函数f(x)的值域;同理可求得当x≥1时,减函数f(x)= ![]() 的值域;(Ⅱ)函数f(x)是(﹣∞,+∞)上的减函数,三个条件需同时成立,①
的值域;(Ⅱ)函数f(x)是(﹣∞,+∞)上的减函数,三个条件需同时成立,① ![]() ≥1,②0<a<1,③12﹣(4a+1)1﹣8a+4≥0,从而可解得实数a的取值范围.
≥1,②0<a<1,③12﹣(4a+1)1﹣8a+4≥0,从而可解得实数a的取值范围.
【考点精析】认真审题,首先需要了解函数单调性的性质(函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集),还要掌握函数的值(函数值的求法:①配方法(二次或四次);②“判别式法”;③反函数法;④换元法;⑤不等式法;⑥函数的单调性法)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P—ABCD中,平面PAD⊥底面ABCD,其中底面ABCD为等腰梯形,AD∥BC,PA=AB=BC=CD=2,PD=2
 ,PA⊥PD,Q为PD的中点.
,PA⊥PD,Q为PD的中点.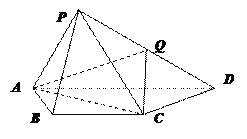
(Ⅰ)证明:CQ∥平面PAB;
(Ⅱ)求直线PD与平面AQC所成角的正弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知动点P(x,y)满足方程xy=1(x>0).
(Ⅰ)求动点P到直线l:x+2y﹣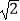 =0距离的最小值;
=0距离的最小值;
(Ⅱ)设定点A(a,a),若点P,A之间的最短距离为2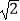 ,求满足条件的实数a的取值.
,求满足条件的实数a的取值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 cosx(sinx+cosx). (Ⅰ)若0<α<
cosx(sinx+cosx). (Ⅰ)若0<α<  ,且sinα=
,且sinα=  ,求f(α)的值;
,求f(α)的值;
(Ⅱ)求函数f(x)的最小正周期及单调递增区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C:(x﹣3)2+(y﹣4)2=4,直线l过定点A(1,0).
(1)若l与圆C相切,求l的方程;
(2)若l与圆C相交于P、Q两点,若|PQ|=2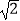 ,求此时直线l的方程.
,求此时直线l的方程. -
科目: 来源: 题型:
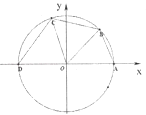
查看答案和解析>>【题目】如图所示,已知点A(1,0),D(﹣1,0),点B,C在单位圆O上,且∠BOC=
 .
. 
(Ⅰ)若点B(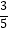 ,
, 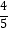 ),求cos∠AOC的值;
),求cos∠AOC的值;
(Ⅱ)设∠AOB=x(0<x<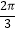 ),四边形ABCD的周长为y,将y表示成x的函数,并求出y的最大值.
),四边形ABCD的周长为y,将y表示成x的函数,并求出y的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的几何体中,四边形ABCD是平行四边形,∠ABD=90°,EB⊥平面ABCD,EF∥AB,AB=2,EB=
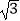 ,EF=1,BC=
,EF=1,BC= 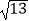 ,且M是BD的中点..
,且M是BD的中点.. 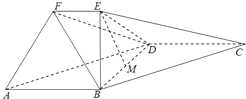
(1)求证:EM∥平面ADF;
(2)求直线DF和平面ABCD所成角的正切值;
(3)求二面角D﹣AF﹣B的大小.
相关试题

