【题目】在直角坐标系xOy中,直线l的参数方程为 ,(为参数),曲线C的参数方程为
,(为参数),曲线C的参数方程为 (α为参数).
(α为参数).
(Ⅰ)已知在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为(3,![]() ),判断点P与直线l位置关系;
),判断点P与直线l位置关系;
(Ⅱ)设点Q是曲线C上的一个动点,求它到直线l的距离的最小值.
参考答案:
【答案】(Ⅰ)点![]() 在直线
在直线![]() 上;
上;
(Ⅱ)![]() .
.
【解析】
(1)把极坐标系下的点![]() 化为直角坐标得点
化为直角坐标得点![]() ,把点
,把点![]() 代入直线
代入直线![]() 的方程
的方程![]() ,即可求解
,即可求解
(2)设出点Q的坐标,代入点到直线的距离公式,求出函数的最小值即为距离的最小值
(1)把极坐标系下的点![]() 化为直角坐标得点
化为直角坐标得点![]() .
.
因为点![]() 的直角坐标满足直线
的直角坐标满足直线![]() 的方程
的方程![]() ,
,
所以点![]() 在直线
在直线![]() 上.
上.
(2)因为点Q在曲线C上,可设点Q的坐标为![]() ,从而点Q到直线
,从而点Q到直线![]() 的距离为
的距离为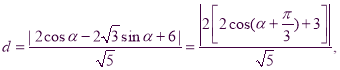
由此得,当![]() 时,
时,![]() 取得最小值,且最小值为
取得最小值,且最小值为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
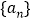 的前
的前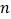 项和
项和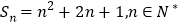 .
.(1)求数列
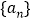 的通项公式;
的通项公式;(2)求数列
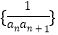 的前
的前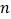 项和
项和 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列四个命题:
①若样本数据
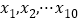 的方差为
的方差为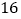 ,则数据
,则数据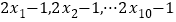 的方差为
的方差为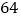 ;
;②“平面向量
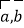 的夹角为锐角,则
的夹角为锐角,则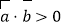 ”的逆命题为真命题;
”的逆命题为真命题;③命题“
 ,均有
,均有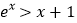 ”的否定是“
”的否定是“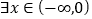 ,均有
,均有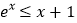 ”;
”;④
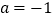 是直线
是直线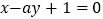 与直线
与直线 平行的必要不充分条件.
平行的必要不充分条件.其中正确的命题个数是( )
A.
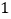 B.
B. 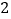 C.
C. 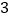 D.
D. 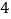
-
科目: 来源: 题型:
查看答案和解析>>【题目】在研究吸烟与患肺癌的关系中,通过收集数据、整理分析数据得“吸烟与患肺癌有关”的结论,并且在犯错误的概率不超过0.01的前提下认为这个结论是成立的,下列说法中正确的是( )
A.100个吸烟者中至少有99人患有肺癌
B.1个人吸烟,那么这个人有99%的概率患有肺癌
C.在100个吸烟者中一定有患肺癌的人
D.在100个吸烟者中可能一个患肺癌的人也没有
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四面体
 的四个顶点都在半径为
的四个顶点都在半径为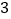 的球面上,
的球面上,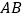 是球的直径,且
是球的直径,且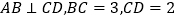 ,则四面体
,则四面体 的体积为( )
的体积为( )A.
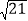 B.
B. 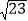 C.
C. 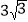 D.
D. 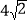
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2017·江苏高考)如图,在三棱锥ABCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E,F(E与A,D不重合)分别在棱AD,BD上,且EF⊥AD.

求证:(1)EF∥平面ABC;
(2)AD⊥AC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C:
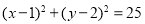 ,直线
,直线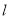 :
: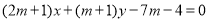
(1)求证:直线
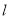 过定点;
过定点;(2)判断该定点与圆的位置关系;
(3)当m为何值时,直线
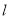 被圆C截得的弦最长.
被圆C截得的弦最长.
相关试题

