【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为矩形,
为矩形,![]() 平面
平面![]() ,
,![]() 是
是![]() 的中点.
的中点.

(1)证明:![]() //平面
//平面![]() ;
;
(2)设![]() ,三棱锥
,三棱锥![]() 的体积
的体积![]() ,求
,求![]() 到平面
到平面![]() 的距离.
的距离.
参考答案:
【答案】(1)详见解析(2) ![]()
【解析】
试题分析:(1)连结BD、AC相交于O,连结OE,则PB∥OE,由此能证明PB∥平面ACE.(2)以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,利用向量法能求出A到平面PBD的距离
试题解析:(I)设BD交AC于点O,连结EO。
因为ABCD为矩形,所以O为BD的中点。
又E为PD的中点,所以EO∥PB
又EO![]() 平面AEC,PB
平面AEC,PB![]() 平面AEC
平面AEC
所以PB∥平面AEC。
(II)![]()
由![]() ,可得
,可得![]() .
.
作![]() 交
交![]() 于
于![]() 。
。
由题设易知![]() ,所以
,所以![]()
故![]() ,
,
又![]() 所以
所以![]() 到平面
到平面![]() 的距离为
的距离为![]()
法2:等体积法
![]()
由![]() ,可得
,可得![]() .
.
由题设易知![]() ,得BC
,得BC![]()
假设![]() 到平面
到平面![]() 的距离为d,
的距离为d,
又因为PB=![]()
所以![]()
又因为![]() (或
(或![]() ),
),
![]() ,
,
所以![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线
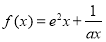 (
(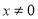 ,
,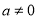 )在
)在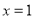 处的切线与直线
处的切线与直线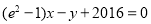 平行.
平行.(1)讨论
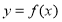 的单调性;
的单调性;(2)若
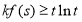 在
在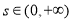 ,
,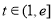 上恒成立,求实数
上恒成立,求实数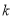 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业共有20条生产线,由于受生产能力和技术水平等因素的影响,会产生一定量的次品.根据经验知道,每台机器产生的次品数
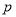 万件与每台机器的日产量
万件与每台机器的日产量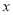 万件
万件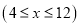 之间满足关系:
之间满足关系: 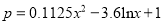 .已知每生产1万件合格的产品可以以盈利3万元,但每生产1万件次品将亏损1万元.
.已知每生产1万件合格的产品可以以盈利3万元,但每生产1万件次品将亏损1万元.(Ⅰ)试将该企业每天生产这种产品所获得的利润
 表示为
表示为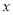 的函数;
的函数;(Ⅱ)当每台机器的日产量为多少时,该企业的利润最大,最大为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】设数列{an}的前n项和为Sn,且首项a1≠3,an+1=Sn+3n(n∈N*).
(1)求证:数列{Sn-3n}是等比数列;
(2)若{an}为递增数列,求a1的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设△ABC的内角A,B,C的对边分别为a,b,c,若c=2
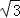 ,sinB=2sinA.
,sinB=2sinA.(1)若C=
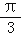 ,求a,b的值;
,求a,b的值;(2)若cosC=
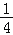 ,求△ABC的面积.
,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为了解广告投入对销售收益的影响,在若干地区各投入
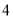 万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从
万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从 开始计数的.
开始计数的.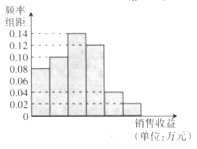
(Ⅰ)根据频率分布直方图计算图中各小长方形的宽度;
(Ⅱ)估计该公司投入
 万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);(Ⅲ)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入x(单位:万元)
1
2
3
4
5
销售收益y(单位:万元)
2
3
2
7
表中的数据显示,
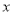 与
与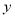 之间存在线性相关关系,请将(Ⅱ)的结果填入空白栏,并计算
之间存在线性相关关系,请将(Ⅱ)的结果填入空白栏,并计算 关于
关于 的回归方程.
的回归方程.回归直线的斜率和截距的最小二乘估计公式分别为
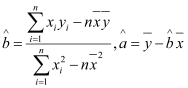 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】北京市为了缓解交通压力,计划在某路段实施“交通限行”,为调查公众对该路段“交通限行”的态度,某机构从经过该路段的人员中随机抽查了80人进行调查,将调查情况进行整理,制成下表:
年龄(岁)
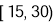
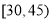
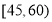
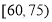
人数
24
26
16
14
赞成人数
12
14
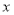
3
(1)若经过该路段的人员对“交通限行”的赞成率为0.40,求
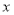 的值;
的值;(2)在(1)的条件下,若从年龄在
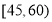 ,
,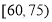 内的两组赞成“交通限行”的人中在随机选取2人进行进一步的采访,求选中的2人中至少有1人来自
内的两组赞成“交通限行”的人中在随机选取2人进行进一步的采访,求选中的2人中至少有1人来自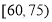 内的概率.
内的概率.
相关试题

