【题目】某公司为了解广告投入对销售收益的影响,在若干地区各投入![]() 万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从
万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从![]() 开始计数的.
开始计数的.
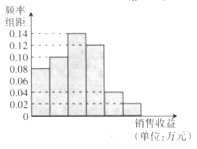
(Ⅰ)根据频率分布直方图计算图中各小长方形的宽度;
(Ⅱ)估计该公司投入![]() 万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
(Ⅲ)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入x(单位:万元) | 1 | 2 | 3 | 4 | 5 |
销售收益y(单位:万元) | 2 | 3 | 2 | 7 |
表中的数据显示,![]() 与
与![]() 之间存在线性相关关系,请将(Ⅱ)的结果填入空白栏,并计算
之间存在线性相关关系,请将(Ⅱ)的结果填入空白栏,并计算![]() 关于
关于![]() 的回归方程.
的回归方程.
回归直线的斜率和截距的最小二乘估计公式分别为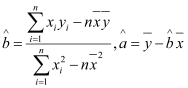 .
.
参考答案:
【答案】(Ⅰ)2(Ⅱ)5(Ⅲ) ![]()
【解析】
试题分析:(1)由频率分布直方图各小长方形面积总和为1,建立方程,即可求得结论;(2)利用组中值,求出对应销售收益的平均值;(3)利用公式求出b,a,即可计算y关于x的回归方程
试题解析:(Ⅰ) 设各小长方形的宽度为![]() ,
,
由频率分布直方图各小长方形面积总和为1,
可知![]() ,
,
故![]() ;
;
(Ⅱ) 由(Ⅰ)知各小组依次是![]() ,
,
其中点分别为![]() ,
,
对应的频率分别为![]() ,
,
故可估计平均值为
![]() ;
;
(Ⅲ) 空白栏中填5. 由题意可知,
![]()
![]() ,
,
![]() ,
,![]() ,
,
根据公式,可求得![]() ,
,
![]() ,
,
即回归直线的方程为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设数列{an}的前n项和为Sn,且首项a1≠3,an+1=Sn+3n(n∈N*).
(1)求证:数列{Sn-3n}是等比数列;
(2)若{an}为递增数列,求a1的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 中,底面
中,底面 为矩形,
为矩形, 平面
平面 ,
, 是
是 的中点.
的中点.
(1)证明:
 //平面
//平面 ;
;(2)设
 ,三棱锥
,三棱锥 的体积
的体积 ,求
,求 到平面
到平面 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】设△ABC的内角A,B,C的对边分别为a,b,c,若c=2
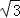 ,sinB=2sinA.
,sinB=2sinA.(1)若C=
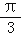 ,求a,b的值;
,求a,b的值;(2)若cosC=
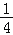 ,求△ABC的面积.
,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】北京市为了缓解交通压力,计划在某路段实施“交通限行”,为调查公众对该路段“交通限行”的态度,某机构从经过该路段的人员中随机抽查了80人进行调查,将调查情况进行整理,制成下表:
年龄(岁)
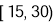
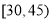
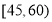
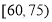
人数
24
26
16
14
赞成人数
12
14
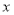
3
(1)若经过该路段的人员对“交通限行”的赞成率为0.40,求
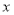 的值;
的值;(2)在(1)的条件下,若从年龄在
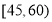 ,
,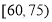 内的两组赞成“交通限行”的人中在随机选取2人进行进一步的采访,求选中的2人中至少有1人来自
内的两组赞成“交通限行”的人中在随机选取2人进行进一步的采访,求选中的2人中至少有1人来自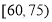 内的概率.
内的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
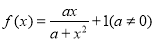 .
.(Ⅰ)若函数
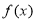 图象在点
图象在点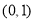 处的切线方程为
处的切线方程为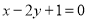 ,求
,求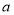 的值;
的值;(Ⅱ)求函数
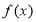 的极值;
的极值;(Ⅲ)若
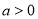 ,
,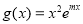 ,且对任意的
,且对任意的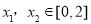 ,
,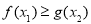 恒成立,求实数
恒成立,求实数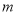 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,a=b·cos C+c·cos B,其中a,b,c分别为角A,B,C的对边,在四面体PABC中,S1,S2,S3,S分别表示△PAB,△PBC,△PCA,△ABC的面积,α,β,γ依次表示面PAB,面PBC,面PCA与底面ABC所成二面角的大小.写出对四面体性质的猜想,并证明你的结论


相关试题

