【题目】已知曲线![]() (
(![]() ,
,![]() )在
)在![]() 处的切线与直线
处的切线与直线![]() 平行.
平行.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() 在
在![]() ,
,![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() 在
在![]() ,
,![]() 上单调递增,在
上单调递增,在![]() ,
,![]() 上单调递减;(2)
上单调递减;(2)![]() .
.
【解析】
试题分析:(1)求出![]() ,
, ![]() 得增区间,
得增区间,![]() 得减区间;(2)
得减区间;(2)![]() 在
在![]() ,
,![]() 上恒成立等价于
上恒成立等价于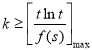
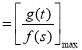 ,故只需求出
,故只需求出![]() 的最小值和
的最小值和![]() 的最大值,分别利用导数研究两函数的单调性,求出最值即可.
的最大值,分别利用导数研究两函数的单调性,求出最值即可.
试题解析:(1)由条件可得![]() ,∴
,∴![]() ,
,
由![]() ,可得
,可得![]() ,
,
由![]() ,可得
,可得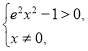 解得
解得![]() 或
或![]() ;
;
由![]() ,可得
,可得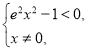 解得
解得![]() 或
或![]() .
.
所以![]() 在
在![]() ,
,![]() 上单调递增,在
上单调递增,在![]() ,
,![]() 上单调递减.
上单调递减.
(2)令![]() ,当
,当![]() ,
,![]() 时,
时,![]() ,
,![]() ,
,
由![]() ,可得
,可得![]() 在
在![]() ,
,![]() 时恒成立,
时恒成立,
即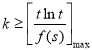
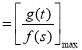 ,故只需求出
,故只需求出![]() 的最小值和
的最小值和![]() 的最大值.
的最大值.
由(1)可知,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
故![]() 的最小值为
的最小值为![]() ,
,
由![]() 可得
可得![]() 在区间
在区间![]() 上恒成立,
上恒成立,
所以![]() 在
在![]() 上的最大值为
上的最大值为![]() ,
,
所以只需![]() ,
,
所以实数![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
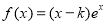 (
(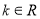 ).
).(1)求
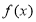 的单调区间和极值;
的单调区间和极值;(2)求
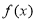 在
在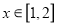 上的最小值.
上的最小值.(3)设
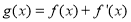 ,若对
,若对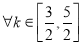 及
及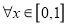 有
有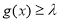 恒成立,求实数
恒成立,求实数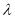 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P﹣ABCD中,△PAB是正三角形,四边形ABCD是矩形,且平面PAB⊥平面ABCD,PA=2,PC=4.
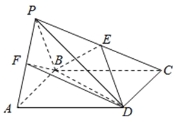
(Ⅰ)若点E是PC的中点,求证:PA∥平面BDE;
(Ⅱ)若点F在线段PA上,且FA=λPA,当三棱锥B﹣AFD的体积为
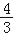 时,求实数λ的值.
时,求实数λ的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
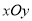 中,过点
中,过点 的直线与抛物线
的直线与抛物线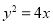 相交于点
相交于点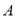 、
、 两点,设
两点,设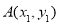 ,
,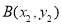 .
.(1)求证:
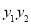 为定值;
为定值;(2)是否存在平行于
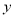 轴的定直线被以
轴的定直线被以 为直径的圆截得的弦长为定值?如果存在,求出该直线方程和弦长,如果不存在,说明理由.
为直径的圆截得的弦长为定值?如果存在,求出该直线方程和弦长,如果不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业共有20条生产线,由于受生产能力和技术水平等因素的影响,会产生一定量的次品.根据经验知道,每台机器产生的次品数
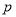 万件与每台机器的日产量
万件与每台机器的日产量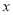 万件
万件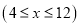 之间满足关系:
之间满足关系: 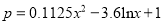 .已知每生产1万件合格的产品可以以盈利3万元,但每生产1万件次品将亏损1万元.
.已知每生产1万件合格的产品可以以盈利3万元,但每生产1万件次品将亏损1万元.(Ⅰ)试将该企业每天生产这种产品所获得的利润
 表示为
表示为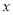 的函数;
的函数;(Ⅱ)当每台机器的日产量为多少时,该企业的利润最大,最大为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】设数列{an}的前n项和为Sn,且首项a1≠3,an+1=Sn+3n(n∈N*).
(1)求证:数列{Sn-3n}是等比数列;
(2)若{an}为递增数列,求a1的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 中,底面
中,底面 为矩形,
为矩形, 平面
平面 ,
, 是
是 的中点.
的中点.
(1)证明:
 //平面
//平面 ;
;(2)设
 ,三棱锥
,三棱锥 的体积
的体积 ,求
,求 到平面
到平面 的距离.
的距离.
相关试题

