【题目】已知函数![]() ,
,![]() 的图象经过
的图象经过![]() 和
和![]() 两点,如图所示,且函数
两点,如图所示,且函数![]() 的值域为
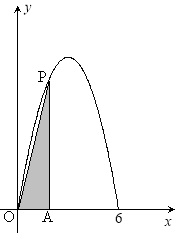
的值域为![]() .过该函数图象上的动点
.过该函数图象上的动点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,连接
,连接![]() .
.
(I)求函数![]() 的解析式;
的解析式;
(Ⅱ)记![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值.
的最大值.
参考答案:
【答案】(I)![]() ;(II)三角形面积的最大值为16.
;(II)三角形面积的最大值为16.
【解析】
试题分析:(I)用待定系数法.由抛物线的对称性及题设可知,函数![]() 的对称轴为
的对称轴为![]() ,顶点为
,顶点为![]() .
.
将顶点坐标及点(0,0),(0,6)的坐标代入解析式得关于a,b,c方程组,解此方程组,便可得 ![]() 的解析式.
的解析式.
(II)用三角形面积公式求得三角形的面积与t之间的函数关系式,然后利用导数可求得![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值.
的最大值.
试题解析:(I)由已知可得函数![]() 的对称轴为
的对称轴为![]() ,顶点为
,顶点为![]() . 2分
. 2分
方法一:由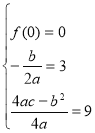
得![]() 5分
5分
得![]() 6分
6分
方法二:设![]() 4分
4分
由![]() ,得
,得![]() 5分
5分
![]() 6分
6分
(II)![]() 8分
8分
![]() 9分
9分
列表得:
|
| 4 |
|
| + | 0 | - |
|
| 极大值 |
|
11分
由上表可得![]() 时,三角形面积取得最大值
时,三角形面积取得最大值
即![]() 13分
13分
-
科目: 来源: 题型:
查看答案和解析>>【题目】几个孩子在一棵枯树上玩耍,他们均不慎失足下落.已知
(
 )甲在下落的过程中依次撞击到树枝
)甲在下落的过程中依次撞击到树枝 ,
, ,
,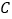 ;
;(
 )乙在下落的过程中依次撞击到树枝
)乙在下落的过程中依次撞击到树枝 ,
, ,
,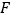 ;
;(
 )丙在下落的过程中依次撞击到树枝
)丙在下落的过程中依次撞击到树枝 ,
, ,
,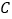 ;
;(
 )丁在下落的过程中依次撞击到树枝
)丁在下落的过程中依次撞击到树枝 ,
, ,
, ;
;(
 )戊在下落的过程中依次撞击到树枝
)戊在下落的过程中依次撞击到树枝 ,
,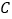 ,
, .
.倒霉和李华在下落的过程中撞到了从
 到
到 的所有树枝,根据以上信息,在李华下落的过程中,和这
的所有树枝,根据以上信息,在李华下落的过程中,和这 根树枝不同的撞击次序有( )种.
根树枝不同的撞击次序有( )种.A.
 B.
B.  C.
C.  D.
D. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在正方体
 中,侧面对角线
中,侧面对角线 ,
, 上分别有一点E,F,且
上分别有一点E,F,且 ,则直线EF与平面ABCD所成的角的大小为( )
,则直线EF与平面ABCD所成的角的大小为( )
A.0°B.60°C.45°D.30°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 是正三角形,EA,CD都垂直于平面ABC,且
是正三角形,EA,CD都垂直于平面ABC,且 ,
, ,F是BE的中点,
,F是BE的中点,
求证:(1)
 平面ABC;
平面ABC;(2)
 平面EDB.
平面EDB.(3)求几何体
 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=lnx+1.
(Ⅰ)证明:当x>0时,f(x)≤x;
(Ⅱ)设 ,若g(x)≥0对x>0恒成立,求实数a的取值范围.
,若g(x)≥0对x>0恒成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,梯形ABCD内接于⊙O,AD∥BC,过点C作⊙O的切线,交BD的延长线于点P,交AD的延长线于点E.
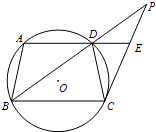
(1)求证:AB2=DEBC;
(2)若BD=9,AB=6,BC=9,求切线PC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某销售公司拟招聘一名产品推销员,有如下两种工资方案:
方案一:每月底薪2000元,每销售一件产品提成15元;
方案二:每月底薪3500元,月销售量不超过300件,没有提成,超过300件的部分每件提成30元.
(1)分别写出两种方案中推销员的月工资
 (单位:元)与月销售产品件数
(单位:元)与月销售产品件数 的函数关系式;
的函数关系式;(2)从该销售公司随机选取一名推销员,对他(或她)过去两年的销售情况进行统计,得到如下统计表:
月销售产品件数

300
400
500
600
700
次数
2
4
9
5
4
把频率视为概率,分别求两种方案推销员的月工资超过11090元的概率.
相关试题

