【题目】如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°. 
(1)求证:平面PBD⊥平面PAC;
(2)求点A到平面PBD的距离;
(3)求二面角A﹣PB﹣D的余弦值.
参考答案:
【答案】
(1)证明:设AC与BD交于O点
∵ABCD是菱形,∴AC⊥BD
以OA、OB所在直线分别x轴,y轴.以过O且垂直平面ABCD的直线为z轴,建立如图的空间直角坐标系,
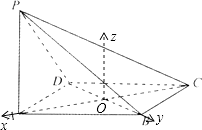
则 ![]()
∵ ![]()
∴ ![]()
∴DB⊥AP
∵AC⊥BD,AC∩AP=A
∴DB⊥平面PAC,又DB平面PDB
∴平面PBD⊥平面PAC
(2)解:设平面PDB的法向量为 ![]() ,
, ![]()
由 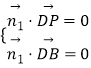 ,∴
,∴ ![]()
令z1=1得 ![]()
∵ ![]()
∴点A到平面PBD的距离  =
= ![]()
(3)解:设平面ABP的法向量 ![]() ,
, ![]()
∵ 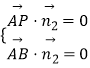 ,∴
,∴ ![]()
∴ ![]()
∴ 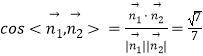
∴二面角A﹣PB﹣D的余弦值为 ![]()
【解析】(1)先证明AC⊥BD,再利用向量的方法证明DB⊥AP,从而可得DB⊥平面PAC,利用面面垂直的判定可得面PBD⊥平面PAC;(2)求出平面PDB的法向量为 ![]() ,
, ![]() ,从而可求点A到平面PBD的距离;(3)求出平面ABP的法向量
,从而可求点A到平面PBD的距离;(3)求出平面ABP的法向量 ![]() ,利用向量的夹角公式,即可求得二面角A﹣PB﹣D的余弦值.
,利用向量的夹角公式,即可求得二面角A﹣PB﹣D的余弦值.
【考点精析】解答此题的关键在于理解平面与平面垂直的判定的相关知识,掌握一个平面过另一个平面的垂线,则这两个平面垂直.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数g(x)=
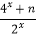 是奇函数,f(x)=log4(4x+1)﹣mx是偶函数.
是奇函数,f(x)=log4(4x+1)﹣mx是偶函数.
(1)求m+n的值;
(2)设h(x)=f(x)+ x,若g(x)>h[log4(2a+1)]对任意x≥1恒成立,求实数a的取值范围.
x,若g(x)>h[log4(2a+1)]对任意x≥1恒成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的二次方程x2+2mx+2m+1=0.
(1)若方程有两个正根,求m的取值范围.
(2)若方程有两根,其中一根在区间(﹣1,0)内,另一根在区间(1,3)内,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】现有甲,乙,丙,丁四位同学课余参加巴蜀爱心社和巴蜀文学风的活动,每人参加且只能参加一个社团的活动,并且参加每个社团都是等可能的.
(1)求巴蜀爱心社和巴蜀文学风都至少有1人参加的概率;
(2)求甲,乙在同一个社团,丙,丁不在同一个社团的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数函数f(x)=(
 )
)  .
.
(1)求函数f(x)的值域
(2)求函数的单调递减区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2+2ax+3.
(1)若f(x)在(﹣∞, ]是减函数,在[
]是减函数,在[  ,+∞)是增函数,求函数f(x)在区间[﹣1,5]的最大值和最小值.
,+∞)是增函数,求函数f(x)在区间[﹣1,5]的最大值和最小值.
(2)求实数a的取值范围,使f(x)在区间[﹣5,5]上是单调函数,并指出相应的单调性. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
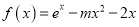
(1)若
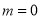 ,讨论
,讨论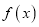 的单调性;
的单调性;(2)若
 ,证明:当
,证明:当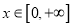 时,
时, 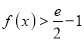
相关试题

