【题目】已知函数![]()
(1)若![]() ,讨论
,讨论![]() 的单调性;
的单调性;
(2)若![]() ,证明:当
,证明:当![]() 时,
时, ![]()
参考答案:
【答案】(1)在![]() 上单调递减,在
上单调递减,在 ![]() 上单调递增;(2)详见解析.
上单调递增;(2)详见解析.
【解析】试题分析:(1)当![]() 时,
时, ![]() ,利用导数与单调性的有关知识,可求得函数的单调区间.(2)对函数
,利用导数与单调性的有关知识,可求得函数的单调区间.(2)对函数![]() 求两次导数,利用二阶导数判读出一阶导数单调递增有唯一零点,设出这个零点,得到
求两次导数,利用二阶导数判读出一阶导数单调递增有唯一零点,设出这个零点,得到![]() 的单调区间和最小值.构造函数
的单调区间和最小值.构造函数![]() ,同样利用二阶导数判断出
,同样利用二阶导数判断出![]() 的单调区间,由此求得
的单调区间,由此求得![]() 的值域.
的值域.
试题解析:
(1)当![]() 时,
时, ![]() .
. ![]() ,令
,令![]() ,得
,得![]() .
.
易知![]() 在
在![]() 上单调递减,
上单调递减, ![]() 在
在![]() 上单调递增.
上单调递增.
(2)证明: ![]() ,
, ![]() .
.
当![]() 时,
时, ![]() ,故
,故![]() ,故
,故![]() 单调递增.
单调递增.
又![]() ,
,
故存在唯一的![]() ,使得
,使得![]() ,即
,即![]() ,
,
且当![]() 时,
时, ![]() ,故
,故![]() 单调递减,
单调递减,
当![]() 时,
时, ![]() ,故
,故![]() 单调递增.
单调递增.
故![]() .
.
因为![]() 是方程
是方程![]() 的根,故
的根,故![]() .
.
故![]() .
.
令![]() ,
, ![]() ,
, ![]() .
.
故![]() 在(0,1)上单调递减,故g
在(0,1)上单调递减,故g![]() ,
,
故![]() 在(0,1)上单调递减,∴
在(0,1)上单调递减,∴![]() ,故
,故![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.

(1)求证:平面PBD⊥平面PAC;
(2)求点A到平面PBD的距离;
(3)求二面角A﹣PB﹣D的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数函数f(x)=(
 )
)  .
.
(1)求函数f(x)的值域
(2)求函数的单调递减区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2+2ax+3.
(1)若f(x)在(﹣∞, ]是减函数,在[
]是减函数,在[  ,+∞)是增函数,求函数f(x)在区间[﹣1,5]的最大值和最小值.
,+∞)是增函数,求函数f(x)在区间[﹣1,5]的最大值和最小值.
(2)求实数a的取值范围,使f(x)在区间[﹣5,5]上是单调函数,并指出相应的单调性. -
科目: 来源: 题型:
查看答案和解析>>【题目】若全集U=R,函数y=
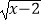 +
+ 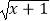 的定义域为A,函数y=
的定义域为A,函数y= 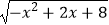 的值域为B.
的值域为B.
(1)求集合A,B;
(2)求(UA)∩(UB). -
科目: 来源: 题型:
查看答案和解析>>【题目】设集合A={x|x2+ax﹣12=0},B={x|x2+bx+c=0},且A≠B,A∪B={﹣3,4},A∩B={﹣3},求实数b,c的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面
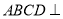 平面
平面 ,四边形
,四边形 为菱形,四边形
为菱形,四边形 为矩形,
为矩形,  ,
,  分别是
分别是 ,
,  的中点,
的中点, 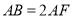 ,
,  .
.(Ⅰ)求证:
 平面
平面 ;
;(Ⅱ)若三棱锥
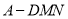 的体积为
的体积为 ,求
,求 的长.
的长.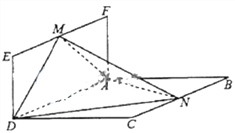
相关试题

