【题目】已知函数函数f(x)=( ![]() )
) ![]() .
.
(1)求函数f(x)的值域
(2)求函数的单调递减区间.
参考答案:
【答案】
(1)解:根据题意:函数f(x)=( ![]() )
) ![]() 是复合函数,
是复合函数,
令﹣x2﹣4x+2=t,则函数f(x)=( ![]() )
) ![]() 转化为g(t)=
转化为g(t)= ![]() ,可知函数g(t)在其定义域内是减函数.
,可知函数g(t)在其定义域内是减函数.
根据二次函数的性质可知:
函数t:开口向下,对称轴x=﹣2,
当x=﹣2时,函数t取得最大值为6.
故得t∈(﹣∞,6].
那么函数g(t)= ![]() 的最小值为g(6)max=
的最小值为g(6)max= ![]() ,即函数f(x)的最小值为
,即函数f(x)的最小值为 ![]() .
.
故得函数f(x)的值域为[ ![]() ,+∞)
,+∞)
(2)解:由(1)可知:函数t在x∈(﹣∞,﹣2)上是单调递增,在x∈(﹣2,+∞)上单调递减.
根据复合函数的单调性“同增异减”可得:
∴函数f(x)=( ![]() )
) ![]() 的单调递减区间为(﹣∞,﹣2)
的单调递减区间为(﹣∞,﹣2)
【解析】(1)根据题意f(x)是复合函数,将其分解成基本函数,利用复合函数的单调性求值域.(2)根据复合函数的单调性“同增异减”可得答案.
【考点精析】解答此题的关键在于理解函数的值域的相关知识,掌握求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的,以及对函数的单调性的理解,了解注意:函数的单调性是函数的局部性质;函数的单调性还有单调不增,和单调不减两种.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的二次方程x2+2mx+2m+1=0.
(1)若方程有两个正根,求m的取值范围.
(2)若方程有两根,其中一根在区间(﹣1,0)内,另一根在区间(1,3)内,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】现有甲,乙,丙,丁四位同学课余参加巴蜀爱心社和巴蜀文学风的活动,每人参加且只能参加一个社团的活动,并且参加每个社团都是等可能的.
(1)求巴蜀爱心社和巴蜀文学风都至少有1人参加的概率;
(2)求甲,乙在同一个社团,丙,丁不在同一个社团的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.

(1)求证:平面PBD⊥平面PAC;
(2)求点A到平面PBD的距离;
(3)求二面角A﹣PB﹣D的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2+2ax+3.
(1)若f(x)在(﹣∞, ]是减函数,在[
]是减函数,在[  ,+∞)是增函数,求函数f(x)在区间[﹣1,5]的最大值和最小值.
,+∞)是增函数,求函数f(x)在区间[﹣1,5]的最大值和最小值.
(2)求实数a的取值范围,使f(x)在区间[﹣5,5]上是单调函数,并指出相应的单调性. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
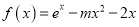
(1)若
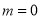 ,讨论
,讨论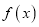 的单调性;
的单调性;(2)若
 ,证明:当
,证明:当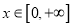 时,
时, 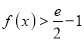
-
科目: 来源: 题型:
查看答案和解析>>【题目】若全集U=R,函数y=
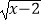 +
+ 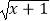 的定义域为A,函数y=
的定义域为A,函数y= 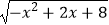 的值域为B.
的值域为B.
(1)求集合A,B;
(2)求(UA)∩(UB).
相关试题

