搜索
【题目】如图，在半径为3m的 
圆形（O为圆心）铝皮上截取一块矩形材料OABC，其中点B在圆弧上，点A、C在两半径上，现将此矩形铝皮OABC卷成一个以AB为母线的圆柱形罐子的侧面（不计剪裁和拼接损耗），设矩形的边长AB=xm，圆柱的体积为Vm3 ．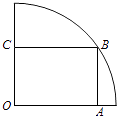 
（1）写出体积V关于x的函数关系式，并指出定义域；
（2）当x为何值时，才能使做出的圆柱形罐子体积V最大？最大体积是多少？
参考答案：
【答案】
（1）解：连接OB，在Rt△OAB中，∵AB=x，∴OA= 
，
设圆柱底面半径为r，则 =2πr，
即4π2r2=9﹣x2，
∴V=πr2x= 
，其中0＜x＜3
（2）解：由V′= 
=0及0＜x＜3，得x= 
，
列表如下：
x | （0， |
| （ |
V′ | + | 0 | ﹣ |
V | 极大值 |
所以当x= 时，V有极大值，也是最大值为 
．…（14分）
答：当x为 m时，做出的圆柱形罐子体积最大，最大体积是 m3．
【解析】（1）连接OB，在Rt△OAB中，由AB=x，利用勾股定理可得OA= ，设圆柱底面半径为r，则 =2πr，即可得出r．利用V=πr2x（其中0＜x＜30）即可得出．（2）利用导数V′，得出其单调性，即可得出结论．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某产品关税与市场供应量P的关系近似地满足：P（x）=2
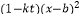（其中t为关税的税率，且t∈[0， 
]，x为市场价格，b，k为正常数），当t= 
时，市场供应量曲线如图所示： 
（1）根据函数图象求k，b的值；
（2）若市场需求量Q，它近似满足Q（x）=2
．当P=Q时的市场价格为均衡价格，为使均衡价格控制在不低于9元的范围内，求税率t的最小值． -
科目： 来源： 题型：
查看答案和解析>>【题目】若函数f（x）=x3﹣
x2+bx+c在x=1时取得极值，且当x∈[﹣1，2]时，f（x）＜c2恒成立．
（1）求实数b的值；
（2）求实数c的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】
袋中有形状和大小完全相同的四种不同颜色的小球，每种颜色的小球各有4个，分别编号为1，2，3，4．现从袋中随机取两个球．
（Ⅰ）若两个球颜色不同，求不同取法的种数；
（Ⅱ）在（1）的条件下，记两球编号的差的绝对值为随机变量X，求随机变量X的概率分布与数学期望．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四棱锥P－ABCD中，PA⊥平面ABCD，AB⊥AD，AD∥BC，AP＝AB＝AD＝1．
（Ⅰ）若直线PB与CD所成角的大小为
，求BC的长；（Ⅱ）求二面角B－PD－A的余弦值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】
已知数列{an}的各项均为正数，记数列{an}的前n项和为Sn，数列{an2}的前n项和为Tn，且3Tn＝Sn2＋2Sn，n∈N*．
（Ⅰ）求a1的值；
（Ⅱ）求数列{an}的通项公式；
（Ⅲ）若k，t∈N*，且S1，Sk－S1，St－Sk成等比数列，求k和t的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=x+
（x＞0，m＞0）和函数g（x）=a|x﹣b|+c（x∈R，a＞0，b＞0）．问：
（1）证明：f（x）在（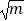
，+∞）上是增函数；
（2）把函数g1（x）=|x|和g2（x）=|x﹣1|写成分段函数的形式，并画出它们的图象，总结出g2（x）的图象是如何由g1（x）的图象得到的．请利用上面你的结论说明：g（x）的图象关于x=b对称；
（3）当m=1，b=2，c=0时，若f（x）＞g（x）对于任意的x＞0恒成立，求a的取值范围．
相关试题
