【题目】在如图所示的四棱锥![]() 中,四边形
中,四边形![]() 为正方形,
为正方形,![]() ,
,![]() 平面
平面![]() ,且
,且![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 的中点,
的中点,![]() .
.
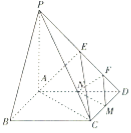
⑴证明:![]() 平面
平面![]() ;
;
⑵若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
参考答案:
【答案】⑴证明见解析;⑵![]() .
.
【解析】
试题分析:⑴做辅助线,由![]() 为
为![]() 中点,
中点,![]() 为
为![]() 中点
中点![]()
![]() .又
.又![]()
![]()
![]() 为
为![]() 中点,又
中点,又![]() ,
,![]()
![]()
![]() 为
为![]() 中点
中点![]()
![]()
![]()
![]()
![]()
![]() 平面
平面![]() ;⑵由
;⑵由![]() 平面
平面![]()
![]()
![]() ,又
,又![]()
![]()
![]() 平面
平面![]() .以
.以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系,求出平面
轴建立空间直角坐标系,求出平面![]() 的一个法向量
的一个法向量![]() ,平面
,平面![]() 的法向量为
的法向量为![]()
![]()
![]() . 由图可知,二面角
. 由图可知,二面角![]() 为钝角
为钝角![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]() .
.
试题解析:⑴证明:连结![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,连结
,连结![]() 、
、![]() ,
,
∵![]() 为
为![]() 中点,
中点,![]() 为
为![]() 中点,∴
中点,∴![]() .……………………2分
.……………………2分
又![]() ,∴
,∴![]() 为
为![]() 中点,又
中点,又![]() ,
,![]() ,∴
,∴![]() 为
为![]() 中点,
中点,
∴![]() ,∴
,∴![]() .……………………………………4分
.……………………………………4分
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .………………………………5分
.………………………………5分
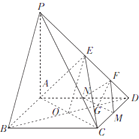
⑵解:∵![]() 平面
平面![]() ,∴
,∴![]() ,又
,又![]() ,
,![]() ,
,
∴![]() 平面
平面![]() .……………………………………6分
.……………………………………6分
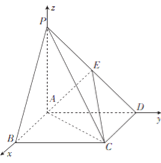
如图 ,以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
则![]() ,
,
则![]() ,
,![]() ,………………………………7分
,………………………………7分
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 的一个法向量
的一个法向量![]() .…………8分
.…………8分
设平面![]() 的法向量为
的法向量为![]() ,
,
则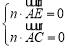 ,即
,即![]() ,…………………………9分
,…………………………9分
令![]() ,则
,则![]() ,
,![]() ,∴
,∴![]() ,…………10分
,…………10分
∴![]() .……………………………………11分
.……………………………………11分
由图可知,二面角![]() 为钝角,
为钝角,
∴二面角![]() 的余弦值为
的余弦值为![]() .……………………………………12分
.……………………………………12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数


(1)若函数
 的图像在
的图像在 处的切线
处的切线 垂直于直线
垂直于直线 ,求实数
,求实数 的值及直线
的值及直线 的方程;
的方程;(2)求函数
 的单调区间;
的单调区间;(3)若
 ,求证:
,求证: 
-
科目: 来源: 题型:
查看答案和解析>>【题目】交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为
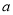 元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就是越高,具体浮动情况如下表:
元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就是越高,具体浮动情况如下表:交强险浮动因素和浮动费率比率表
浮动因素
浮动比率
上一个年度未发生有责任道路交通事故
下浮10%
上两个年度未发生有责任道路交通事故
下浮20%
上三个及以上年度未发生有责任道路交通事故
下浮30%
上一个年度发生一次有责任不涉及死亡的道路交通事故
0%
上一个年度发生两次及两次以上有责任道路交通事故
上浮10%
上一个年度发生有责任道路交通死亡事故
上浮30%
某机构为了 某一品牌普通6座以下私家车的投保情况,随机抽取了60辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型
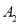
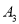
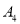
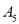
数量
10
5
5
20
15
5
以这60辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
(1)按照我国《机动车交通事故责任强制保险条例》汽车交强险价格的规定,
 ,记
,记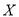 为某同学家的一辆该品牌车在第四年续保时的费用,求
为某同学家的一辆该品牌车在第四年续保时的费用,求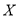 的分布列与数学期望;(数学期望值保留到个位数字)
的分布列与数学期望;(数学期望值保留到个位数字)(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车,假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元:
①若该销售商购进三辆(车龄已满三年)该品牌二手车,求这三辆车中至多有一辆事故车的概率;
②若该销售商一次购进100辆(车龄已满三年)该品牌二手车,求他获得利润的期望值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
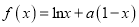 ,
, 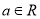 .
.(I)求
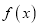 的单调区间;
的单调区间;(II)若对任意的
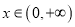 ,都有
,都有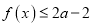 ,求实数
,求实数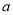 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】一座圆拱桥,当水面在如图所示位置时,拱顶离水面2米,水面宽12米,当水面下降1米后,水面宽多少米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
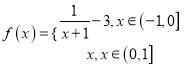 ,且g(x)=f(x)-mx-m在(-1,1]内有且仅有两个不同的零点,则实数m的取值范围是________.
,且g(x)=f(x)-mx-m在(-1,1]内有且仅有两个不同的零点,则实数m的取值范围是________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
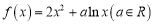 .
.⑴讨论函数
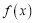 的单调性;
的单调性;⑵若
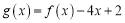 存在两个极值点,且
存在两个极值点,且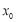 是函数
是函数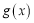 的极小值点,求证:
的极小值点,求证: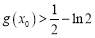 .
.
相关试题

