【题目】交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为![]() 元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就是越高,具体浮动情况如下表:
元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就是越高,具体浮动情况如下表:
交强险浮动因素和浮动费率比率表 | ||
浮动因素 | 浮动比率 | |
| 上一个年度未发生有责任道路交通事故 | 下浮10% |
| 上两个年度未发生有责任道路交通事故 | 下浮20% |
| 上三个及以上年度未发生有责任道路交通事故 | 下浮30% |
| 上一个年度发生一次有责任不涉及死亡的道路交通事故 | 0% |
| 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮10% |
| 上一个年度发生有责任道路交通死亡事故 | 上浮30% |
某机构为了 某一品牌普通6座以下私家车的投保情况,随机抽取了60辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型 |
|
|
|
|
|
|
数量 | 10 | 5 | 5 | 20 | 15 | 5 |
以这60辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
(1)按照我国《机动车交通事故责任强制保险条例》汽车交强险价格的规定, ![]() ,记
,记![]() 为某同学家的一辆该品牌车在第四年续保时的费用,求
为某同学家的一辆该品牌车在第四年续保时的费用,求![]() 的分布列与数学期望;(数学期望值保留到个位数字)
的分布列与数学期望;(数学期望值保留到个位数字)
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车,假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元:
①若该销售商购进三辆(车龄已满三年)该品牌二手车,求这三辆车中至多有一辆事故车的概率;
②若该销售商一次购进100辆(车龄已满三年)该品牌二手车,求他获得利润的期望值.
参考答案:
【答案】(1)![]() (2)①
(2)①![]() ②5000
②5000
【解析】试题分析:(1)根据题意,首先确定X的所有可能取值,然后利用统计表格,借助古典概型的公式计算对应的概率,进而利用期望公式求解;(2)利用独立重复实验的概率计算公式求解满足条件的概率,明确![]() 为该销售商购进并销售一辆二手车的利润的可能性,得到分布列和利润期望值.
为该销售商购进并销售一辆二手车的利润的可能性,得到分布列和利润期望值.
(Ⅰ)由题意可知X的可能取值为![]() ,
,
由统计数据可知:
![]() ,
,
![]() .
.
所以![]() 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
所以![]() .
.
(Ⅱ) ①由统计数据可知任意一辆该品牌车龄已满三年的二手车为事故车的概率为![]() ,三辆车中至多有一辆事故车的概率为
,三辆车中至多有一辆事故车的概率为![]() .
.
![]() 为该销售商购进并销售一辆二手车的利润,
为该销售商购进并销售一辆二手车的利润, ![]() 的可能取值为
的可能取值为![]() .
.
所以![]() 的分布列为:
的分布列为:
|
|
|
|
|
|
所以![]() .
.
所以该销售商一次购进100辆该品牌车龄已满三年的二手车获得利润的期望值为![]() 万元.
万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家商场对同一种商品展开促销活动,对购买该商品的顾客两家商场的奖励方案如下:
甲商场:顾客转动如图所示转盘,当指针指向阴影部分(图中两个阴影部分均为扇形,且每个扇形圆心角均为
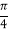 ,边界忽略不计)即为中奖.
,边界忽略不计)即为中奖.乙商场:从装有4个白球,4个红球和4个篮球的盒子中一次性摸出3球(这些球初颜色外完全相同),如果摸到的是3个不同颜色的球,即为中奖.

(Ⅰ)试问:购买该商品的顾客在哪家商场中奖的可能性大?说明理由;
(Ⅱ)记在乙商场购买该商品的顾客摸到篮球的个数为
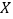 ,求
,求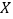 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
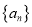 的前
的前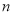 项和为
项和为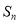 ,且满足
,且满足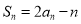 ,求数列
,求数列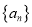 的通项公式.勤于思考的小红设计了下面两种解题思路,请你选择其中一种并将其补充完整.
的通项公式.勤于思考的小红设计了下面两种解题思路,请你选择其中一种并将其补充完整.思路1:先设
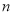 的值为1,根据已知条件,计算出
的值为1,根据已知条件,计算出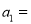 _________,
_________, 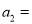 __________,
__________, 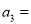 _________.
_________.猜想:
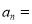 _______.
_______.然后用数学归纳法证明.证明过程如下:
①当
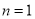 时,________________,猜想成立
时,________________,猜想成立②假设
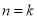 (
(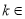 N*)时,猜想成立,即
N*)时,猜想成立,即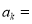 _______.
_______.那么,当
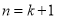 时,由已知
时,由已知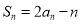 ,得
,得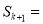 _________.
_________.又
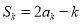 ,两式相减并化简,得
,两式相减并化简,得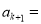 _____________(用含
_____________(用含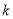 的代数式表示).
的代数式表示).所以,当
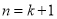 时,猜想也成立.
时,猜想也成立.根据①和②,可知猜想对任何
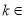 N*都成立.
N*都成立.思路2:先设
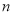 的值为1,根据已知条件,计算出
的值为1,根据已知条件,计算出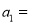 _____________.
_____________.由已知
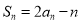 ,写出
,写出 与
与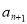 的关系式:
的关系式: 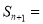 _____________________,
_____________________,两式相减,得
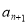 与
与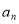 的递推关系式:
的递推关系式: 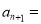 ____________________.
____________________.整理:
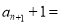 ____________.
____________.发现:数列
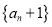 是首项为________,公比为_______的等比数列.
是首项为________,公比为_______的等比数列.得出:数列
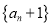 的通项公式
的通项公式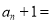 ____,进而得到
____,进而得到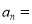 ____________.
____________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数


(1)若函数
 的图像在
的图像在 处的切线
处的切线 垂直于直线
垂直于直线 ,求实数
,求实数 的值及直线
的值及直线 的方程;
的方程;(2)求函数
 的单调区间;
的单调区间;(3)若
 ,求证:
,求证: 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
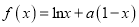 ,
, 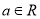 .
.(I)求
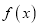 的单调区间;
的单调区间;(II)若对任意的
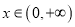 ,都有
,都有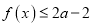 ,求实数
,求实数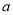 的取值范围.
的取值范围. -
科目: 来源: 题型:
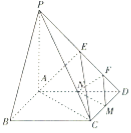
查看答案和解析>>【题目】在如图所示的四棱锥
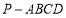 中,四边形
中,四边形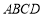 为正方形,
为正方形,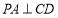 ,
,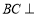 平面
平面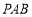 ,且
,且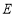 、
、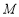 、
、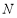 分别为
分别为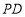 、
、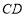 、
、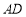 的中点,
的中点,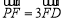 .
.
⑴证明:
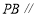 平面
平面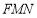 ;
;⑵若
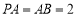 ,求二面角
,求二面角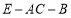 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】一座圆拱桥,当水面在如图所示位置时,拱顶离水面2米,水面宽12米,当水面下降1米后,水面宽多少米?

相关试题

