【题目】已知圆![]() 经过点A(-2,0),B(0,2),且圆心
经过点A(-2,0),B(0,2),且圆心![]() 在直线y=x上,又直线l:y=kx+1与圆
在直线y=x上,又直线l:y=kx+1与圆![]() 相交于P、Q两点.
相交于P、Q两点.
(1)求圆![]() 的方程;
的方程;
(2)若![]() ,求实数k的值;
,求实数k的值;
(3)过点![]() 作动直线
作动直线![]() 交圆
交圆![]() 于
于![]() ,
,![]() 两点.试问:在以
两点.试问:在以![]() 为直径的所有圆中,是否存在这样的圆
为直径的所有圆中,是否存在这样的圆![]() ,使得圆
,使得圆![]() 经过点
经过点![]() ?若存在,求出圆
?若存在,求出圆![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在圆
;(3)存在圆![]() 或
或![]() ,使得圆
,使得圆![]() 经过点
经过点![]() .
.
【解析】
试题分析:(1)根据题意设出圆心![]() 和半径
和半径![]() ,列出
,列出![]() 和
和![]() 的方程,求得圆的方程;(2)根据
的方程,求得圆的方程;(2)根据![]() ,
,
求得![]() ,所以圆心到直线
,所以圆心到直线![]() 的距离为
的距离为![]() ,求得
,求得![]() 的值;(3)若圆
的值;(3)若圆![]() 经过点
经过点![]() ,则必有
,则必有![]() 即
即![]() ①,当直线
①,当直线![]() 的斜率不存在时,显然满足题意得圆,当直线
的斜率不存在时,显然满足题意得圆,当直线![]() 的斜率存在时,设其斜率为
的斜率存在时,设其斜率为![]() ,直线
,直线![]() 的方程为:
的方程为:![]() ,代入圆
,代入圆![]() 的方程,由韦达定理,得到
的方程,由韦达定理,得到![]() 的值,联立①解得
的值,联立①解得![]() 的值,存在所求的圆,进而得到所求的圆的方程.
的值,存在所求的圆,进而得到所求的圆的方程.
试题解析:(1)设圆心C(a,a),半径为r.因为圆C经过点A(-2,0),B(0,2),所以|AC|=|BC|=r,易得a=0,r=2,所以圆C的方程是![]() . 3分
. 3分
(2)因为![]() ·
·![]() =2×2×cos〈
=2×2×cos〈![]() ,
,![]() 〉=-2,且
〉=-2,且![]() 与
与![]() 的夹角为∠POQ,
的夹角为∠POQ,
所以cos∠POQ=-![]() ,∠POQ=120°,所以圆心C到直线l:kx-y+1=0的距离d=1,
,∠POQ=120°,所以圆心C到直线l:kx-y+1=0的距离d=1,
又d=![]() ,所以
,所以![]() . 7分
. 7分
(联立直线与圆的方程求解酌情给分)
(3)(ⅰ)当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 经过圆
经过圆![]() 的圆心
的圆心![]() ,此时直线
,此时直线![]() 与圆
与圆![]() 的交点为
的交点为![]() ,
,![]() ,
,![]() 即为圆
即为圆![]() 的直径,而点
的直径,而点![]() 在圆
在圆![]() 上,即圆
上,即圆![]() 也是满足题意的圆 8分
也是满足题意的圆 8分
(ⅱ)当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() ,由
,由![]() ,
,
消去![]() 整理,得
整理,得![]() ,由△
,由△![]() ,得
,得![]() 或
或![]() .
.
设![]() ,则有
,则有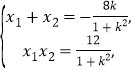 ① 9分
① 9分
由①得![]() , ②
, ②
![]() , ③
, ③
若存在以![]() 为直径的圆
为直径的圆![]() 经过点
经过点![]() ,则
,则![]() ,所以
,所以![]() ,
,
因此![]() ,即
,即![]() , 10分
, 10分
则![]() ,所以
,所以![]() ,
,![]() ,满足题意. 12分
,满足题意. 12分
此时以![]() 为直径的圆的方程为
为直径的圆的方程为![]() ,
,
即![]() ,亦即
,亦即![]() . 13分
. 13分
综上,在以![]() 为直径的所有圆中,存在圆
为直径的所有圆中,存在圆![]() :
:![]() 或
或
![]() ,使得圆
,使得圆![]() 经过点
经过点![]() . 14分
. 14分
-
科目: 来源: 题型:
查看答案和解析>>【题目】在去年的足球甲
 联赛上,一队每场比赛平均失球数是1.5,全年比赛失球个数的标准差为1.1;二队每场比赛平均失球数是2.1,全年失球个数的标准差是0.4,你认为下列说法中正确的个数有( )
联赛上,一队每场比赛平均失球数是1.5,全年比赛失球个数的标准差为1.1;二队每场比赛平均失球数是2.1,全年失球个数的标准差是0.4,你认为下列说法中正确的个数有( )①平均来说一队比二队防守技术好;②二队比一队防守技术水平更稳定;③一队防守有时表现很差,有时表现又非常好;④二队很少不失球.
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (其中
(其中 )的图象与x轴的相邻两个交点之间的距离为
)的图象与x轴的相邻两个交点之间的距离为 ,且图象上一个最高点为
,且图象上一个最高点为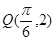
(1)求
 的解析式;
的解析式;(2)当
 ,求
,求 的值域.
的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市拟定2016年城市建设A,B,C三项重点工程,该市一大型城建公司准备参加这三个工程的竞标,假设这三个工程竞标成功与否相互独立,该公司对A,B,C三项重点工程竞标成功的概率分别为a,b,
 (a>b),已知三项工程都竞标成功的概率为
(a>b),已知三项工程都竞标成功的概率为 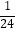 ,至少有一项工程竞标成功的概率为
,至少有一项工程竞标成功的概率为  .
.
(1)求a与b的值;
(2)公司准备对该公司参加A,B,C三个项目的竞标团队进行奖励,A项目竞标成功奖励2万元,B项目竞标成功奖励4万元,C项目竞标成功奖励6万元,求竞标团队获得奖励金额的分布列与数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
 的焦点在
的焦点在 轴上,离心率为
轴上,离心率为 ,抛物线
,抛物线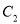 的焦点在
的焦点在 轴上,
轴上,  的中心和
的中心和 的顶点均为原点,点
的顶点均为原点,点 在
在 上,点
上,点 在
在 上,
上,(1)求曲线
 ,
,  的标准方程;
的标准方程;(2)请问是否存在过抛物线
 的焦点
的焦点 的直线
的直线 与椭圆
与椭圆 交于不同两点
交于不同两点 ,使得以线段
,使得以线段 为直径的圆过原点
为直径的圆过原点 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】给出以下命题,其中真命题的个数是( )
①若“
 或
或 ”是假命题,则“
”是假命题,则“ 且
且 ”是真命题;
”是真命题;②命题“若
 ,则
,则 或
或 ”为真命题;
”为真命题;③已知空间任意一点
 和不共线的三点
和不共线的三点 ,
, ,
, ,若
,若 ,则
,则 ,
, ,
, ,
, 四点共面;
四点共面;④直线
 与双曲线
与双曲线 交于
交于 ,
, 两点,若
两点,若 ,则这样的直线有3条;
,则这样的直线有3条;A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校1800名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50名学生组成一个样本,将测试结果按如下方式分成五组:第一组
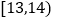 ,第二组
,第二组 ……,第五组
……,第五组 ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.
(1)请估计学校1800名学生中,成绩属于第四组的人数;
(2)若成绩小于15秒认为良好,求该样本中在这次百米测试中成绩良好的人数;
(3)请根据频率分布直方图,求样本数据的众数、平均数.
相关试题

