【题目】某市拟定2016年城市建设A,B,C三项重点工程,该市一大型城建公司准备参加这三个工程的竞标,假设这三个工程竞标成功与否相互独立,该公司对A,B,C三项重点工程竞标成功的概率分别为a,b, ![]() (a>b),已知三项工程都竞标成功的概率为
(a>b),已知三项工程都竞标成功的概率为 ![]() ,至少有一项工程竞标成功的概率为
,至少有一项工程竞标成功的概率为 ![]() .
.
(1)求a与b的值;
(2)公司准备对该公司参加A,B,C三个项目的竞标团队进行奖励,A项目竞标成功奖励2万元,B项目竞标成功奖励4万元,C项目竞标成功奖励6万元,求竞标团队获得奖励金额的分布列与数学期望.
参考答案:
【答案】
(1)解:由题意得 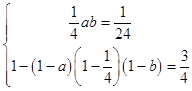 ,
,
由a>b,解得a= ![]() ,b=
,b= ![]()
(2)解:由题意,令竞标团队获得奖励金额为随机变量X,则X的值可以为0,2,4,6,8,10,
P(X=0)= ![]() ,
,
P(X=2)= ![]() =
= ![]() ,
,
P(X=4)= ![]() =
= ![]() ,
,
P(X=6)= ![]() =
= ![]() ,
,
P(X=8)= ![]() =
= ![]() ,
,
P(X=10)= ![]() =
= ![]() ,
,
P(X=12)= ![]() =
= ![]() ,
,
∴X的分布列为:
X | 0 | 2 | 4 | 6 | 8 | 10 | 12 |
P |
|
|
|
|
|
|
|
E(X)= ![]() +
+ ![]() =
= ![]() .
.
【解析】(1)由题意利用相互独立事件概率乘法公式和对立事件概率计算公式列出方程组,能求出a与b的值.(2)由题意,令竞标团队获得奖励金额为随机变量X,则X的值可以为0,2,4,6,8,10,分别求出相应的概率,由此能求出X的分布列和E(X).
【考点精析】解答此题的关键在于理解离散型随机变量及其分布列的相关知识,掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数
 是定义在
是定义在 上的奇函数,且
上的奇函数,且 为偶函数,当
为偶函数,当 时,
时, ,若
,若 有三个零点,则实数
有三个零点,则实数 的取值集合是( )
的取值集合是( )A.

B.

C.

D.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在去年的足球甲
 联赛上,一队每场比赛平均失球数是1.5,全年比赛失球个数的标准差为1.1;二队每场比赛平均失球数是2.1,全年失球个数的标准差是0.4,你认为下列说法中正确的个数有( )
联赛上,一队每场比赛平均失球数是1.5,全年比赛失球个数的标准差为1.1;二队每场比赛平均失球数是2.1,全年失球个数的标准差是0.4,你认为下列说法中正确的个数有( )①平均来说一队比二队防守技术好;②二队比一队防守技术水平更稳定;③一队防守有时表现很差,有时表现又非常好;④二队很少不失球.
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (其中
(其中 )的图象与x轴的相邻两个交点之间的距离为
)的图象与x轴的相邻两个交点之间的距离为 ,且图象上一个最高点为
,且图象上一个最高点为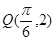
(1)求
 的解析式;
的解析式;(2)当
 ,求
,求 的值域.
的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 经过点A(-2,0),B(0,2),且圆心
经过点A(-2,0),B(0,2),且圆心 在直线y=x上,又直线l:y=kx+1与圆
在直线y=x上,又直线l:y=kx+1与圆 相交于P、Q两点.
相交于P、Q两点.(1)求圆
 的方程;
的方程;(2)若
 ,求实数k的值;
,求实数k的值;(3)过点
 作动直线
作动直线 交圆
交圆 于
于 ,
, 两点.试问:在以
两点.试问:在以 为直径的所有圆中,是否存在这样的圆
为直径的所有圆中,是否存在这样的圆 ,使得圆
,使得圆 经过点
经过点 ?若存在,求出圆
?若存在,求出圆 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
 的焦点在
的焦点在 轴上,离心率为
轴上,离心率为 ,抛物线
,抛物线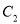 的焦点在
的焦点在 轴上,
轴上,  的中心和
的中心和 的顶点均为原点,点
的顶点均为原点,点 在
在 上,点
上,点 在
在 上,
上,(1)求曲线
 ,
,  的标准方程;
的标准方程;(2)请问是否存在过抛物线
 的焦点
的焦点 的直线
的直线 与椭圆
与椭圆 交于不同两点
交于不同两点 ,使得以线段
,使得以线段 为直径的圆过原点
为直径的圆过原点 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】给出以下命题,其中真命题的个数是( )
①若“
 或
或 ”是假命题,则“
”是假命题,则“ 且
且 ”是真命题;
”是真命题;②命题“若
 ,则
,则 或
或 ”为真命题;
”为真命题;③已知空间任意一点
 和不共线的三点
和不共线的三点 ,
, ,
, ,若
,若 ,则
,则 ,
, ,
, ,
, 四点共面;
四点共面;④直线
 与双曲线
与双曲线 交于
交于 ,
, 两点,若
两点,若 ,则这样的直线有3条;
,则这样的直线有3条;A. 1 B. 2 C. 3 D. 4
相关试题

