【题目】某学校1800名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50名学生组成一个样本,将测试结果按如下方式分成五组:第一组![]() ,第二组
,第二组![]() ……,第五组
……,第五组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.

(1)请估计学校1800名学生中,成绩属于第四组的人数;
(2)若成绩小于15秒认为良好,求该样本中在这次百米测试中成绩良好的人数;
(3)请根据频率分布直方图,求样本数据的众数、平均数.
参考答案:
【答案】![]() 人
人![]() ;(2)
;(2)![]() 人
人![]() ;
; ![]() 15.70.
15.70.
【解析】试题分析:
(1)利用频率分布直方图能估计学校1800名学生中,成绩属于第四组的人数![]() .(2)利用频率分布直方图能求出该样本在这次百米测试中成绩良好的人数.(3)根据频率分布直方图,能求出样本数据的众数、中位数.
.(2)利用频率分布直方图能求出该样本在这次百米测试中成绩良好的人数.(3)根据频率分布直方图,能求出样本数据的众数、中位数.
解析:
![]() 学校1800名学生中,成绩属于第四组的人数
学校1800名学生中,成绩属于第四组的人数![]() 人
人![]() ;
;
(2)样本在这次百米测试中成绩良好的人数是:![]() 人
人![]() ;
;
![]() 由图可知众数落在第三组
由图可知众数落在第三组![]() ,是
,是![]() ,
,
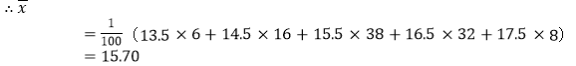 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 经过点A(-2,0),B(0,2),且圆心
经过点A(-2,0),B(0,2),且圆心 在直线y=x上,又直线l:y=kx+1与圆
在直线y=x上,又直线l:y=kx+1与圆 相交于P、Q两点.
相交于P、Q两点.(1)求圆
 的方程;
的方程;(2)若
 ,求实数k的值;
,求实数k的值;(3)过点
 作动直线
作动直线 交圆
交圆 于
于 ,
, 两点.试问:在以
两点.试问:在以 为直径的所有圆中,是否存在这样的圆
为直径的所有圆中,是否存在这样的圆 ,使得圆
,使得圆 经过点
经过点 ?若存在,求出圆
?若存在,求出圆 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
 的焦点在
的焦点在 轴上,离心率为
轴上,离心率为 ,抛物线
,抛物线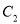 的焦点在
的焦点在 轴上,
轴上,  的中心和
的中心和 的顶点均为原点,点
的顶点均为原点,点 在
在 上,点
上,点 在
在 上,
上,(1)求曲线
 ,
,  的标准方程;
的标准方程;(2)请问是否存在过抛物线
 的焦点
的焦点 的直线
的直线 与椭圆
与椭圆 交于不同两点
交于不同两点 ,使得以线段
,使得以线段 为直径的圆过原点
为直径的圆过原点 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】给出以下命题,其中真命题的个数是( )
①若“
 或
或 ”是假命题,则“
”是假命题,则“ 且
且 ”是真命题;
”是真命题;②命题“若
 ,则
,则 或
或 ”为真命题;
”为真命题;③已知空间任意一点
 和不共线的三点
和不共线的三点 ,
, ,
, ,若
,若 ,则
,则 ,
, ,
, ,
, 四点共面;
四点共面;④直线
 与双曲线
与双曲线 交于
交于 ,
, 两点,若
两点,若 ,则这样的直线有3条;
,则这样的直线有3条;A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】用1,2,3,4,5,6组成数字不重复的六位数,满足1不在左右两端,2,4,6三个偶数中,有且只有两个偶数相邻,则这样的六位数的个数为( )
A.432
B.288
C.216
D.144 -
科目: 来源: 题型:
查看答案和解析>>【题目】设圆(x+1)2+y2=25的圆心为C,A(1,0)是圆内一定点,Q为圆周上任一点.线段AQ的垂直平分线与CQ的连线交于点M,则M的轨迹方程为( )

A.
B.
C.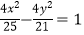
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 过点
过点 ,且与圆
,且与圆 关于直线
关于直线 对称.
对称.(1)求两圆的方程;
(2)若直线
 与直线
与直线 平行,且截距为7,在
平行,且截距为7,在 上取一横坐标为
上取一横坐标为 的点
的点 ,过点
,过点 作圆
作圆 的切线,切点为
的切线,切点为 ,设
,设 中点为
中点为 .
.(ⅰ)若
 ,求
,求 的值;
的值;(ⅱ)是否存在点
 ,使得
,使得 ?若存在,求点
?若存在,求点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
相关试题

