【题目】已知数列{xn}满足:x1=1,xn=xn+1+ln(1+xn+1)(n∈N*),证明:当n∈N*时,
(Ⅰ)0<xn+1<xn;
(Ⅱ)2xn+1﹣xn≤ ![]() ;
;
(Ⅲ) ![]() ≤xn≤
≤xn≤ ![]() .
.
参考答案:
【答案】解:(Ⅰ)用数学归纳法证明:xn>0,
当n=1时,x1=1>0,成立,
假设当n=k时成立,则xk>0,
那么n=k+1时,若xk+1<0,则0<xk=xk+1+ln(1+xk+1)<0,矛盾,
故xn+1>0,
因此xn>0,(n∈N*)
∴xn=xn+1+ln(1+xn+1)>xn+1 ,
因此0<xn+1<xn(n∈N*),
(Ⅱ)由xn=xn+1+ln(1+xn+1)得xnxn+1﹣4xn+1+2xn=xn+12﹣2xn+1+(xn+1+2)ln(1+xn+1),
记函数f(x)=x2﹣2x+(x+2)ln(1+x),x≥0
∴f′(x)= ![]() +ln(1+x)>0,
+ln(1+x)>0,
∴f(x)在(0,+∞)上单调递增,
∴f(x)≥f(0)=0,
因此xn+12﹣2xn+1+(xn+1+2)ln(1+xn+1)≥0,
故2xn+1﹣xn≤ ![]() ;
;
(Ⅲ)∵xn=xn+1+ln(1+xn+1)≤xn+1+xn+1=2xn+1 ,
∴xn≥ ![]() ,
,
由 ![]() ≥2xn+1﹣xn得
≥2xn+1﹣xn得 ![]() ﹣
﹣ ![]() ≥2(
≥2( ![]() ﹣
﹣ ![]() )>0,
)>0,
∴ ![]() ﹣
﹣ ![]() ≥2(
≥2( ![]() ﹣
﹣ ![]() )≥…≥2n﹣1(
)≥…≥2n﹣1( ![]() ﹣
﹣ ![]() )=2n﹣2 ,
)=2n﹣2 ,
∴xn≤ ![]() ,
,
综上所述 ![]() ≤xn≤
≤xn≤ ![]() .
.
【解析】(Ⅰ)用数学归纳法即可证明,
(Ⅱ)构造函数,利用导数判断函数的单调性,把数列问题转化为函数问题,即可证明,
(Ⅲ)由 ![]() ≥2xn+1﹣xn得
≥2xn+1﹣xn得 ![]() ﹣
﹣ ![]() ≥2(
≥2( ![]() ﹣
﹣ ![]() )>0,继续放缩即可证明
)>0,继续放缩即可证明
【考点精析】关于本题考查的利用导数研究函数的单调性和数列的通项公式,需要了解一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能得出正确答案.
在这个区间单调递减;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方体ABCD
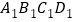 中,以D为原点建立空间直角坐标系,E为B
中,以D为原点建立空间直角坐标系,E为B 的中点,F为
的中点,F为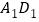 的中点,则下列向量中,能作为平面AEF的法向量的是( )
的中点,则下列向量中,能作为平面AEF的法向量的是( )
A. (1,-2,4) B. (-4,1,-2)
C. (2,-2,1) D. (1,2,-2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方体ABCD
 中,下面结论错误的是( )
中,下面结论错误的是( )
A. BD∥平面C
 B. AC1⊥BD
B. AC1⊥BDC. AC1⊥平面C
 D. 向量
D. 向量 与
与 的夹角为60°
的夹角为60° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正三棱柱ABC﹣A1B1C1中,所有棱长均为1,则点B1到平面ABC1的距离为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知空间中三点A(-2,0,2),B(-1,1,2),C(-3,0,4),设a=
 ,b=
,b= .
.(1)求向量a与向量b的夹角的余弦值;
(2)若ka+b与ka-2b互相垂直,求实数k的值
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱ABC
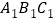 中,AC=3,BC=4,AB=5,A
中,AC=3,BC=4,AB=5,A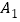 =4.
=4.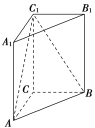
(1)证明:
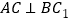 ;
;(2)求二面角
 的余弦值大小.
的余弦值大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】执行如图所示的程序框图,输出的S值为( )

A.2
B.
C.
D.
相关试题

