【题目】已知空间中三点A(-2,0,2),B(-1,1,2),C(-3,0,4),设a=![]() ,b=
,b=![]() .
.
(1)求向量a与向量b的夹角的余弦值;
(2)若ka+b与ka-2b互相垂直,求实数k的值
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
试题分析:(1)第一步,求出两个向量的坐标,第二步,分别计算![]() ,和
,和![]() ,最后代入公式
,最后代入公式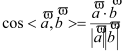 ;
;
(2)方法一,先得到![]() 和
和![]() 的坐标,然后代入数量积的坐标表示,可得
的坐标,然后代入数量积的坐标表示,可得![]() 的值;
的值;
方法二,先计算(![]() )(
)(![]() )
)![]() ,然后代入两个向量的坐标表示,求
,然后代入两个向量的坐标表示,求![]() 的值.
的值.
试题解析:解 (1)∵a=(1,1,0),b=(-1,0,2), ∴a·b=(1,1,0)·(-1,0,2)=-1,
又|a|=![]() =
=![]() , |b|=
, |b|=![]() =
=![]() ,
,
∴cos〈a,b〉=![]() =
=![]() =-
=-![]() , 即向量a与向量b的夹角的余弦值为-
, 即向量a与向量b的夹角的余弦值为-![]() .
.
(2)方法一 ∵ka+b=(k-1,k,2).ka-2b=(k+2,k,-4),且ka+b与ka-2b互相垂直,
∴(k-1,k,2)·(k+2,k,-4)=(k-1)(k+2)+k2-8=0, ∴k=2或k=-![]() ,
,
∴当ka+b与ka-2b互相垂直时,实数k的值为2或-![]() .、
.、
方法二 由(1)知|a|=![]() ,|b|=
,|b|=![]() ,a·b=-1,
,a·b=-1,
∴(ka+b)·(ka-2b)=k2a2-ka·b-2b2=2k2+k-10=0, 得k=2或k=-![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方体ABCD
 中,下面结论错误的是( )
中,下面结论错误的是( )
A. BD∥平面C
 B. AC1⊥BD
B. AC1⊥BDC. AC1⊥平面C
 D. 向量
D. 向量 与
与 的夹角为60°
的夹角为60° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正三棱柱ABC﹣A1B1C1中,所有棱长均为1,则点B1到平面ABC1的距离为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{xn}满足:x1=1,xn=xn+1+ln(1+xn+1)(n∈N*),证明:当n∈N*时,
(Ⅰ)0<xn+1<xn;
(Ⅱ)2xn+1﹣xn≤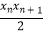 ;
;
(Ⅲ)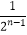 ≤xn≤
≤xn≤ 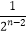 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱ABC
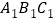 中,AC=3,BC=4,AB=5,A
中,AC=3,BC=4,AB=5,A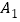 =4.
=4.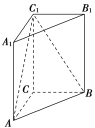
(1)证明:
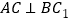 ;
;(2)求二面角
 的余弦值大小.
的余弦值大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】执行如图所示的程序框图,输出的S值为( )

A.2
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,角α与角β均以Ox为始边,它们的终边关于y轴对称,若sinα=
 ,则cos(α﹣β)= .
,则cos(α﹣β)= .
相关试题

