【题目】如图,在直三棱柱ABC![]() 中,AC=3,BC=4,AB=5,A
中,AC=3,BC=4,AB=5,A![]() =4.
=4.
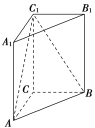
(1)证明:![]() ;
;
(2)求二面角![]() 的余弦值大小.
的余弦值大小.
参考答案:
【答案】⑴见证明;⑵![]()
【解析】
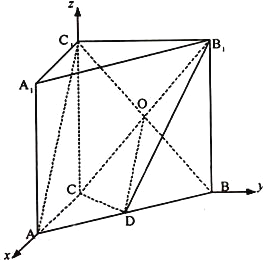
(1)根据AC,BC,CC1两两垂直,建立如图以C为坐标原点,建立空间直角坐标系C﹣xyz,写出要用的点的坐标,根据两个向量的数量级等于0,证出两条线段垂直.
(2)根据所给的两个平面的法向量一个可以直接看出另一个设出根据数量级等于0,求出结果,根据两个平面的法向量所成的角求出两个平面所成的角.
∵直三棱柱ABC﹣A1B1C1,底面三边长AC=3,BC=4,AB=5,
∴AC,BC,CC1两两垂直.
如图以C为坐标原点,建立空间直角坐标系C﹣xyz,则C(0,0,0),A(3,0,0),C1(0,0,4),B(0,4,0),B1(0,4,4). …(2分)
证明:(1)∵![]() =(﹣3,0,0),
=(﹣3,0,0),![]() =(0,﹣4,4),
=(0,﹣4,4),
∴![]()
![]() =0,
=0,
故AC⊥BC1…(4分)
解:(2)平面ABC的一个法向量为![]() =(0,0,1),
=(0,0,1),
设平面C1AB的一个法向量为![]() =(x,y,z),
=(x,y,z),
![]() =(﹣3,0,4),
=(﹣3,0,4),![]() =(﹣3,4,0),
=(﹣3,4,0),
由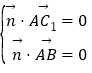 得:
得:![]() …(6分)
…(6分)
令x=4,则z=3,y=3则![]() =(4,3,3).…(7分)
=(4,3,3).…(7分)
故cos<![]() ,
,![]() >=
>=![]() =
=![]() .
.
即二面角![]() ABC的余弦值为
ABC的余弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正三棱柱ABC﹣A1B1C1中,所有棱长均为1,则点B1到平面ABC1的距离为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{xn}满足:x1=1,xn=xn+1+ln(1+xn+1)(n∈N*),证明:当n∈N*时,
(Ⅰ)0<xn+1<xn;
(Ⅱ)2xn+1﹣xn≤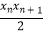 ;
;
(Ⅲ)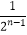 ≤xn≤
≤xn≤ 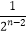 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知空间中三点A(-2,0,2),B(-1,1,2),C(-3,0,4),设a=
 ,b=
,b= .
.(1)求向量a与向量b的夹角的余弦值;
(2)若ka+b与ka-2b互相垂直,求实数k的值
-
科目: 来源: 题型:
查看答案和解析>>【题目】执行如图所示的程序框图,输出的S值为( )

A.2
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,角α与角β均以Ox为始边,它们的终边关于y轴对称,若sinα=
 ,则cos(α﹣β)= .
,则cos(α﹣β)= . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,AB=BC=4,点E在线段AB上.过点E作EF∥BC交AC于点F,将△AEF沿EF折起到△PEF的位置(点A与P重合),使得∠PEB=60°.

(1)求证:EF⊥PB.
(2)试问:当点E在线段AB上移动时,二面角PFCB的平面角的余弦值是否为定值?若是,求出其定值;若不是,说明理由.
相关试题

