【题目】某餐厅通过查阅了最近5次食品交易会参会人数![]() (万人)与餐厅所用原材料数量
(万人)与餐厅所用原材料数量![]() (袋),得到如下统计表:
(袋),得到如下统计表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
参会人数 | 13 | 9 | 8 | 10 | 12 |
原材料 | 32 | 23 | 18 | 24 | 28 |
(1)根据所给5组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(2)已知购买原材料的费用![]() (元)与数量
(元)与数量![]() (袋)的关系为
(袋)的关系为![]() ,
,
投入使用的每袋原材料相应的销售收入为700元,多余的原材料只能无偿返还,据悉本次交易大会大约有15万人参加,根据(1)中求出的线性回归方程,预测餐厅应购买多少袋原材料,才能获得最大利润,最大利润是多少?(注:利润![]() 销售收入
销售收入![]() 原材料费用).
原材料费用).
参考公式:  ,
, ![]() .
.
参考数据: ![]() ,
, ![]() ,
, ![]() .
.
参考答案:
【答案】(1)![]() ;(2)餐厅应该购买36袋原材料,才能使利润获得最大,最大利润为11870元.
;(2)餐厅应该购买36袋原材料,才能使利润获得最大,最大利润为11870元.
【解析】试题分析:(1)根据公式求出b,再将样本中心代入求出a,进而得到回归方程;(2)![]() ,利润为赚的钱减去花出去的钱,根据分段函数的表达式,分段列出利润表达式,分别讨论利润的最值,最终取分段函数中较大的利润值.
,利润为赚的钱减去花出去的钱,根据分段函数的表达式,分段列出利润表达式,分别讨论利润的最值,最终取分段函数中较大的利润值.
解析:
(1)由所给数据可得: ![]() ,
, ![]() ,
,
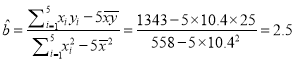 ,
, ![]() ,
,
则![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() .
.
(2)由(1)中求出的线性回归方程知,当![]() 时,
时, ![]() ,即预计需要原材料
,即预计需要原材料![]() 袋,
袋,
因为![]() ,所以当
,所以当![]() 时,
时,
利润![]() ,当
,当![]() 时,
时, ![]() ;
;
当![]() 时,利润
时,利润![]() ,当
,当![]() 时,
时, ![]() .
.
综上所述,餐厅应该购买36袋原材料,才能使利润获得最大,最大利润为11870元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等差数列
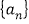 中,
中, ,
,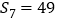 .若记
.若记 表示不超过
表示不超过 的最大整数,(如
的最大整数,(如 ).令
).令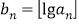 ,则数列
,则数列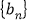 的前2000项和为__________.
的前2000项和为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
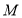 :
: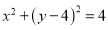 ,点
,点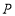 是直线
是直线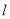 :
: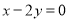 上的一动点,过点
上的一动点,过点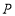 作圆M的切线
作圆M的切线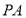 、
、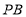 ,切点为
,切点为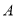 、
、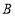 .
.(Ⅰ)当切线PA的长度为
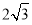 时,求点
时,求点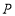 的坐标;
的坐标;(Ⅱ)若
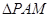 的外接圆为圆
的外接圆为圆 ,试问:当
,试问:当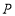 运动时,圆
运动时,圆 是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由;
是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由;(Ⅲ)求线段
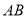 长度的最小值.
长度的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等比数列{an}满足:|a2﹣a3|=10,a1a2a3=125.
(1)求数列{an}的通项公式;
(2)是否存在正整数m,使得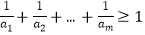 ?若存在,求m的最小值;若不存在,说明理由.
?若存在,求m的最小值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
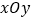 中,抛物线
中,抛物线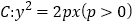 的焦点为
的焦点为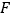 ,点
,点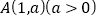 是抛物线
是抛物线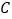 上一点,且
上一点,且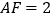 .
.(1)求
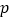 的值;
的值;(2)若
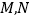 为抛物线
为抛物线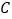 上异于
上异于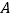 的两点,且
的两点,且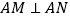 .记点
.记点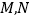 到直线
到直线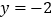 的距离分别为
的距离分别为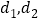 ,求
,求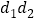 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学一名数学老师对全班50名学生某次考试成绩分男女生进行统计(满分150分),其中120分(含120分)以上为优秀,绘制了如图所示的两个频率分布直方图:

(1)根据以上两个直方图完成下面的
 列联表:
列联表:性别 成绩
优秀
不优秀
总计
男生
女生
总计
(2)根据(1)中表格的数据计算,你有多大把握认为学生的数学成绩与性别之间有关系?

2.072
2.706
3.841
5.024
6.635
7.879
10.828

0.15
0.10
0.05
0.025
0.010
0.005
0.001
附:
 ,其中
,其中 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在底面为矩形的四棱锥
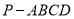 中,
中,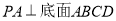 ,
,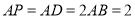 ,且
,且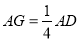 ,其中
,其中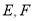 分别是线段
分别是线段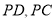 的中点。
的中点。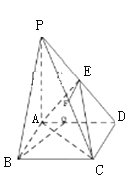
(1)证明:
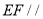 平面
平面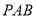
(2)证明:
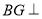 平面
平面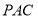
(3)求:直线
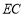 与平面
与平面 所成角的正弦值
所成角的正弦值
相关试题

