【题目】等差数列![]() 中,
中,![]() ,
,![]() .若记
.若记![]() 表示不超过
表示不超过![]() 的最大整数,(如
的最大整数,(如![]() ).令
).令![]() ,则数列
,则数列![]() 的前2000项和为__________.
的前2000项和为__________.
参考答案:
【答案】5445.
【解析】分析:设等差数列{an}的公差为d,由a3+a4=12,S7=49.可得2a1+5d=12,![]() d=49,解出即可得出; bn=[lgan]=[lg(2n﹣1)],n=1,2,3,4,5时,bn=0.6≤n≤50时,bn=1;51≤n≤500时,bn=2;501≤n≤2000时,bn=3.即可得出.
d=49,解出即可得出; bn=[lgan]=[lg(2n﹣1)],n=1,2,3,4,5时,bn=0.6≤n≤50时,bn=1;51≤n≤500时,bn=2;501≤n≤2000时,bn=3.即可得出.
详解:设等差数列{an}的公差为d,∵a3+a4=12,S7=49.
∴2a1+5d=12,![]() d=49,
d=49,
解得a1=1,d=2.
∴an=1+2(n﹣1)=2n﹣1.
bn=[lgan]=[lg(2n﹣1)],
n=1,2,3,4,5时,bn=0.
6≤n≤50时,bn=1;
51≤n≤500时,bn=2;
501≤n≤2000时,bn=3.
∴数列{bn}的前2000项和=45+450×2+1500×3=5445.
故答案为:5445.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某网站从春节期间参与收发网络红包的手机用户中随机抽取10000名进行调查,将受访用户按年龄分成5组:
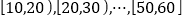 并整理得到如下频率分布直方图:
并整理得到如下频率分布直方图: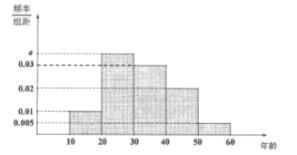
(1)求
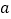 的值;
的值;(2)从春节期间参与收发网络红包的手机用户中随机抽取一人,估计其年龄低于40岁的概率;
(3)估计春节期间参与收发网络红包的手机用户的平均年龄。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,抛物线
中,抛物线 的焦点为
的焦点为 ,点
,点 是抛物线
是抛物线 上一点,且
上一点,且 .
.(1)求
 的值;
的值;(2)若
 为抛物线
为抛物线 上异于
上异于 的两点,且
的两点,且 .记点
.记点 到直线
到直线 的距离分别为
的距离分别为 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)
已知函数
 ,其中
,其中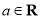 .
.(Ⅰ)当
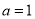 时,求曲线
时,求曲线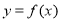 在点
在点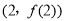 处的切线方程;
处的切线方程;(Ⅱ)当
 时,求函数
时,求函数 的单调区间与极值.
的单调区间与极值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
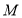 :
: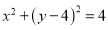 ,点
,点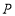 是直线
是直线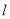 :
: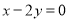 上的一动点,过点
上的一动点,过点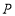 作圆M的切线
作圆M的切线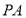 、
、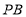 ,切点为
,切点为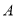 、
、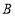 .
.(Ⅰ)当切线PA的长度为
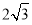 时,求点
时,求点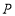 的坐标;
的坐标;(Ⅱ)若
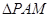 的外接圆为圆
的外接圆为圆 ,试问:当
,试问:当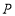 运动时,圆
运动时,圆 是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由;
是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由;(Ⅲ)求线段
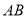 长度的最小值.
长度的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等比数列{an}满足:|a2﹣a3|=10,a1a2a3=125.
(1)求数列{an}的通项公式;
(2)是否存在正整数m,使得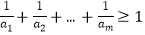 ?若存在,求m的最小值;若不存在,说明理由.
?若存在,求m的最小值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某餐厅通过查阅了最近5次食品交易会参会人数
 (万人)与餐厅所用原材料数量
(万人)与餐厅所用原材料数量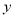 (袋),得到如下统计表:
(袋),得到如下统计表:第一次
第二次
第三次
第四次
第五次
参会人数
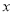 (万人)
(万人)13
9
8
10
12
原材料
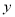 (袋)
(袋)32
23
18
24
28
(1)根据所给5组数据,求出
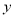 关于
关于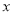 的线性回归方程
的线性回归方程 .
.(2)已知购买原材料的费用
 (元)与数量
(元)与数量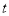 (袋)的关系为
(袋)的关系为 ,
,投入使用的每袋原材料相应的销售收入为700元,多余的原材料只能无偿返还,据悉本次交易大会大约有15万人参加,根据(1)中求出的线性回归方程,预测餐厅应购买多少袋原材料,才能获得最大利润,最大利润是多少?(注:利润
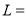 销售收入
销售收入 原材料费用).
原材料费用).参考公式:
 ,
, 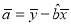 .
.参考数据:
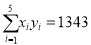 ,
,  ,
, 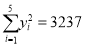 .
.
相关试题

