【题目】已知椭圆C的方程为 ![]() +
+ ![]() =1(a>b>0),双曲线
=1(a>b>0),双曲线 ![]() ﹣
﹣ ![]() =1的一条渐近线与x轴所成的夹角为30°,且双曲线的焦距为4
=1的一条渐近线与x轴所成的夹角为30°,且双曲线的焦距为4 ![]() .
.
(1)求椭圆C的方程;
(2)设F1 , F2分别为椭圆C的左,右焦点,过F2作直线l(与x轴不重合)交于椭圆于A,B两点,线段AB的中点为E,记直线F1E的斜率为k,求k的取值范围.
参考答案:
【答案】
(1)解:由一条渐近线与x轴所成的夹角为30°,则 ![]() =tan30°=
=tan30°= ![]() ,即a2=3b2,
,即a2=3b2,
由2c=4 ![]() .c=2
.c=2 ![]() ,则a2+b2=8,
,则a2+b2=8,
解得:a2=8,b2=2,
∴椭圆的标准方程: ![]()
(2)解:由(1)可知:F2(2,0),直线AB的方程:x=ty+2,A(x1,y1),B(x2,y2),
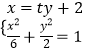 ,整理得:(t2+3)y2+4ty﹣2=0,
,整理得:(t2+3)y2+4ty﹣2=0,
y1+y2=﹣ ![]() ,x1+x2=
,x1+x2= ![]() ,
,
则E( ![]() ,﹣
,﹣ ![]() ),
),
由F1(﹣2,0),则直线F1E的斜率k= 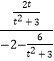 =﹣
=﹣ ![]() ,
,
①当t=0时,k=0,
②当t≠0时,丨k丨= ![]() =
= ![]() ≤
≤ ![]() ,
,
即丨k丨∈(0, ![]() ],
],
∴k的取值范围[﹣ ![]() ,
, ![]() ]
]
【解析】(1)由双曲线的渐近线方程及斜率公式,即可求得a2=3b2,c=2 ![]() ,即a2+b2=8,即可求得a和b的值,求得椭圆方程;(2)设直线AB的方程,代入椭圆方程,利用韦达定理求得斜率丨k丨用t表示,利用基本不等式即可求得k的取值范围.
,即a2+b2=8,即可求得a和b的值,求得椭圆方程;(2)设直线AB的方程,代入椭圆方程,利用韦达定理求得斜率丨k丨用t表示,利用基本不等式即可求得k的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】第35届牡丹花会期间,我班有5名学生参加志愿者服务,服务场所是王城公园和牡丹公园.
(1)若学生甲和乙必须在同一个公园,且甲和丙不能在同一个公园,则共有多少种不同的分配方案?
(2)每名学生都被随机分配到其中的一个公园,设X,Y分别表示5名学生分配到王城公园和牡丹公园的人数,记ξ=|X﹣Y|,求随机变量ξ的分布列和数学期望E(ξ) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形BB1C1C所在平面与底面ABB1N垂直,在直角梯形ABB1N中,AN∥BB1 , AB⊥AN,CB=BA=AN=
 BB1 .
BB1 . 
(1)求证:BN⊥平面C1B1N;
(2)求二面角C﹣C1N﹣B的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( >0,
>0,  ≠1,
≠1,  ≠﹣1),是定义在(﹣1,1)上的奇函数.
≠﹣1),是定义在(﹣1,1)上的奇函数.(1)求实数
 的值;
的值;(2)当
 =1时,判断函数
=1时,判断函数 在(﹣1,1)上的单调性,并给出证明;
在(﹣1,1)上的单调性,并给出证明;(3)若
 且
且 ,求实数
,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
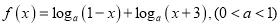 .
.(1)求函数
 的定义域;
的定义域;(2)若函数
 的最小值为
的最小值为 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=xlnx+ax,a∈R.
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若对x>1,f(x)>(b+a﹣1)x﹣b恒成立,求整数b的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知cos(75°+α)=
 ,α是第三象限角,
,α是第三象限角,(1)求sin(75°+α) 的值.
(2)求cos(α-15°) 的值.
(3)求sin(195°-α)+cos(105o-α)的值.
相关试题

