【题目】高三一班、二班各有6名学生去参加学校组织的高中数学竞赛选拔考试,成绩如茎叶图所示.
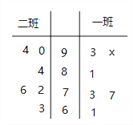
(1)若一班、二班6名学生的平均分相同,求![]() 值;
值;
(2)若将竞赛成绩在![]() 、
、![]() 、
、![]() 内的学生在学校推优时,分别赋分、2分、3分,现在从一班的6名参赛学生中选两名,求推优时,这两名学生赋分的和为4分的概率.
内的学生在学校推优时,分别赋分、2分、3分,现在从一班的6名参赛学生中选两名,求推优时,这两名学生赋分的和为4分的概率.
参考答案:
【答案】(1) x=4 (2) ![]()
【解析】试题分析:(1)由两个班的平均分相等可求得x.(2)由茎叶图可知,一班赋3,2,1分的学生各有2名,不妨分别记为A1,A2, B1,B2, C1,C2,由枚举法可知总共情况15种,满足条件5种,所以概率P=![]() =
=![]() 。
。
试题解析:(Ⅰ)由93+90+x+81+73+77+61=90+94+84+72+76+63,得x=4.
(Ⅱ)由题意知一班赋3,2,1分的学生各有2名,
设赋3分的学生为A1,A2,赋2分的学生为B1,B2,赋1分的学生为C1,C2,
则从6人抽取两人的基本事件为A1A2,A1B1,A1B2,A1C1,A1C2,A2B1,A2B2,A2C1,A2C2,B1B2,B1C1,B1C2,B2C1,B2C2,C1C2共15种,
其中赋分和为4分的有5种,
∴这两名学生赋分的和为4的概率P=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
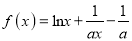 ,
, 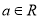 且
且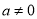 .
.(1)讨论函数
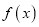 的单调性;
的单调性;(2)当
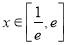 时,试判断函数
时,试判断函数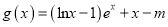 的零点个数.
的零点个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】在公比为q的等比数列{an}中,已知a1=16,且a1,a2+2,a3成等差数列.
(Ⅰ)求q,an;
(Ⅱ)若q<1,求满足a1-a2+a3-…+(-1)2n-1a2n>10的最小的正整数n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥AD,,AC=AD=CD,E是AD的中点.
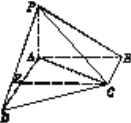
(Ⅰ)证明CE∥平面PAB;
(Ⅱ)证明:平面PAD⊥平面PCE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
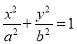 (a>b>0)的离心率为
(a>b>0)的离心率为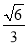 .
.(Ⅰ)若原点到直线x+y-b=0的距离为
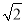 ,求椭圆的方程;
,求椭圆的方程;(Ⅱ)设过椭圆的右焦点且倾斜角为45°的直线l和椭圆交于A,B两点,对于椭圆上任意一点M,总存在实数λ、μ,使等式
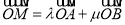 成立,求λ2+μ2的值.
成立,求λ2+μ2的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
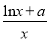 (a∈R).
(a∈R).(Ⅰ)求f(x)的单调区间与极值;
(Ⅱ)若函数f(x)的图象与函数g(x)=1的图象在区间(0,e2]上有两个公共点,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,曲线M的参数方程为
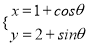 (θ为参数),若以直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线N的极坐标方程为ρsin(θ+
(θ为参数),若以直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线N的极坐标方程为ρsin(θ+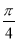 )=
)=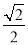 t(其中t为常数).
t(其中t为常数).(Ⅰ)若曲线N与曲线M只有一个公共点,求t的值;
(Ⅱ)当t=-1时,求曲线M上的点与曲线N上的点的最小距离.
相关试题

