【题目】在公比为q的等比数列{an}中,已知a1=16,且a1,a2+2,a3成等差数列.
(Ⅰ)求q,an;
(Ⅱ)若q<1,求满足a1-a2+a3-…+(-1)2n-1a2n>10的最小的正整数n的值.
参考答案:
【答案】(Ⅰ)见解析(Ⅱ)3.
【解析】试题分析:(1)由a1,a2+2,a3成等差数列,可求得公比q,an。(2)由(1)及q<1,可得,an=25-n,可得原不等式左边是等比数列数列![]() 求和。
求和。
试题解析:(Ⅰ)由16+16q2=2(16q+2)得4q2-8q+3=0,q=![]() 或
或![]() ,
,
当q=![]() 时,an=25-n,
时,an=25-n,
当q=![]() 时,an=16(
时,an=16(![]() )n-1.
)n-1.
(Ⅱ)q<1,an=25-n,a1-a2+a3+…+(-1)2n-1a2n=
=![]() [
[![]() ]>10,
]>10,
(![]() )2n<
)2n< ![]() ,2n>4,n>2,正整数n的最小值为3.
,2n>4,n>2,正整数n的最小值为3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了减少雾霾,还城市一片蓝天,某市政府于12月4日到12月31日在主城区实行车辆限号出行政策,鼓励民众不开车低碳出行,某甲乙两个单位各有200名员工,为了了解员工低碳出行的情况,统计了12月5日到12月14日共10天的低碳出行的人数,画出茎叶图如下:
(1)若甲单位数据的平均数是122,求
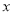 ;
;(2)现从如图的数据中任取4天的数据(甲、乙两单位中各取2天),记其中甲、乙两单位员工低碳出行人数不低于130人的天数为
 ,
, 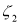 ,令
,令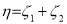 ,求
,求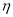 的分布列和期望.
的分布列和期望.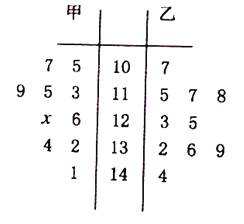
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥
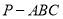 中,平面
中,平面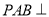 平面
平面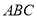 ,
, 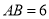 ,
, 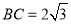 ,
, 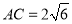 ,
,  分别为线段
分别为线段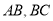 上的点,且
上的点,且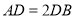 ,
, 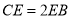 ,
,  .
.(1)求证:
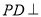 平面
平面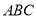 ;
;(2)若
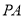 与平面
与平面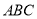 所成的角为
所成的角为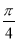 ,求平面
,求平面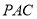 与平面
与平面 所成的锐二面角.
所成的锐二面角.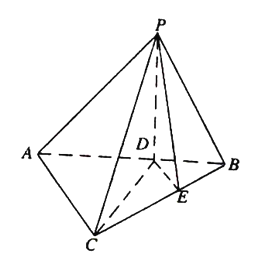
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
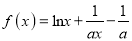 ,
, 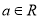 且
且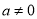 .
.(1)讨论函数
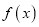 的单调性;
的单调性;(2)当
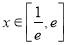 时,试判断函数
时,试判断函数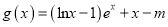 的零点个数.
的零点个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥AD,,AC=AD=CD,E是AD的中点.
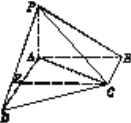
(Ⅰ)证明CE∥平面PAB;
(Ⅱ)证明:平面PAD⊥平面PCE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】高三一班、二班各有6名学生去参加学校组织的高中数学竞赛选拔考试,成绩如茎叶图所示.
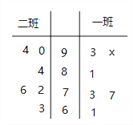
(1)若一班、二班6名学生的平均分相同,求
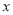 值;
值;(2)若将竞赛成绩在
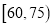 、
、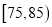 、
、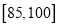 内的学生在学校推优时,分别赋分、2分、3分,现在从一班的6名参赛学生中选两名,求推优时,这两名学生赋分的和为4分的概率.
内的学生在学校推优时,分别赋分、2分、3分,现在从一班的6名参赛学生中选两名,求推优时,这两名学生赋分的和为4分的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
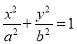 (a>b>0)的离心率为
(a>b>0)的离心率为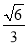 .
.(Ⅰ)若原点到直线x+y-b=0的距离为
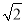 ,求椭圆的方程;
,求椭圆的方程;(Ⅱ)设过椭圆的右焦点且倾斜角为45°的直线l和椭圆交于A,B两点,对于椭圆上任意一点M,总存在实数λ、μ,使等式
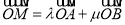 成立,求λ2+μ2的值.
成立,求λ2+μ2的值.
相关试题

