【题目】A. 选修4-1:几何证明选讲
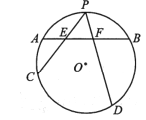
如图,已知![]() 为圆
为圆![]() 的一条弦,点
的一条弦,点![]() 为弧
为弧![]() 的中点,过点
的中点,过点![]() 任作两条弦
任作两条弦![]() 分别交
分别交![]() 于点
于点![]() .
.
求证:![]() .
.
参考答案:
【答案】详见解析.
【解析】试题分析:连结PA,PB,CD,BC,因为∠PAB =∠PCB,
又点P为弧AB的中点,所以∠PAB =∠PBA,所以∠PCB =∠PBA. 又∠DCB =∠DPB,
所以∠PFE =∠PBA+∠DPB =∠PCB+∠DCB =∠PCD,所以E,F,D,C四点共圆.
试题解析:
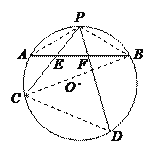
连结PA,PB,CD,BC.
因为∠PAB =∠PCB,
又点P为弧AB的中点,所以∠PAB =∠PBA,
所以∠PCB =∠PBA. 又∠DCB =∠DPB,
所以∠PFE =∠PBA+∠DPB =∠PCB+∠DCB =∠PCD,
所以E,F,D,C四点共圆.
所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出以下说法:①不共面的四点中,任意三点不共线;
②有三个不同公共点的两个平面重合;
③没有公共点的两条直线是异面直线;
④分别和两条异面直线都相交的两条直线异面;
⑤一条直线和两条异面直线都相交,则它们可以确定两个平面.
其中正确结论的序号是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,角A,B,C所对边分别为a,b,c,a=2,B=45°,①当b=
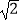 时,三角形有个解;②若三角形有两解,则b的取值范围是 .
时,三角形有个解;②若三角形有两解,则b的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线y=x3,求:
(1)曲线在点P(1,1)处的切线方程;
(2)过点P(1,0)的曲线的切线方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线
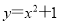 ,问是否存在实数a,使得经过点(1,a)能够作出该曲线的两条切线?若存在求出实数a的取值范围,若不存在,说明理由.
,问是否存在实数a,使得经过点(1,a)能够作出该曲线的两条切线?若存在求出实数a的取值范围,若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】【江西省临川实验学校2017届高三第一次模拟考试数学(文)】已知抛物线
 ,焦点为
,焦点为 ,点
,点 在抛物线
在抛物线 上,且
上,且 到
到 的距离比
的距离比 到直线
到直线 的距离小1.
的距离小1.(1)求抛物线
 的方程;
的方程;(2)若点
 为直线
为直线 上的任意一点,过点
上的任意一点,过点 作抛物线
作抛物线 的切线
的切线 与
与 ,切点分别为
,切点分别为 ,求证:直线
,求证:直线 恒过某一定点.
恒过某一定点. -
科目: 来源: 题型:
查看答案和解析>>【题目】设数列{an}是等差数列,前n项和为Sn , {bn}是单调递增的等比数列,b1=2是a1与a2的等差中项,a3=5,b3=a4+1,若当n≥m时,Sn≤bn恒成立,则m的最小值为 .
相关试题

