【题目】设数列{an}是等差数列,前n项和为Sn , {bn}是单调递增的等比数列,b1=2是a1与a2的等差中项,a3=5,b3=a4+1,若当n≥m时,Sn≤bn恒成立,则m的最小值为 .
参考答案:
【答案】4
【解析】解:∵b1=2是a1与a2的等差中项, ∴a1+a2=4,
∵a3=5,
∴ ![]() ,解得a1=1,d=2,
,解得a1=1,d=2,
则a4=a3+d=5+2=7,
则Sn=n+ ![]() =n2 ,
=n2 ,
则b3=a4+17+1=8,
∵b1=2,
∴公比q2= ![]() ,
,
∵{bn}是单调递增的等比数列,
∴q=2,
则bn=22n﹣1=2n ,
当n=1时,S1≤b1成立,
当n=2时,S2≤b2成立,
当n=3时,S3≤b3不成立,
当n=4时,S4≤b4成立,
当n>4时,Sn≤bn恒成立,
综上当n≥4时,Sn≤bn恒成立,
故m的最小值为4,
所以答案是:4
【考点精析】利用等差数列的性质和等比数列的基本性质对题目进行判断即可得到答案,需要熟知在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列;{an}为等比数列,则下标成等差数列的对应项成等比数列;{an}既是等差数列又是等比数列== {an}是各项不为零的常数列.
-
科目: 来源: 题型:
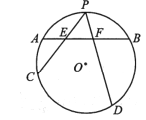
查看答案和解析>>【题目】A. 选修4-1:几何证明选讲
如图,已知
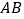 为圆
为圆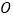 的一条弦,点
的一条弦,点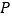 为弧
为弧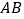 的中点,过点
的中点,过点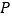 任作两条弦
任作两条弦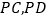 分别交
分别交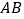 于点
于点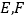 .
.求证:
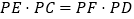 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线
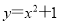 ,问是否存在实数a,使得经过点(1,a)能够作出该曲线的两条切线?若存在求出实数a的取值范围,若不存在,说明理由.
,问是否存在实数a,使得经过点(1,a)能够作出该曲线的两条切线?若存在求出实数a的取值范围,若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】【江西省临川实验学校2017届高三第一次模拟考试数学(文)】已知抛物线
 ,焦点为
,焦点为 ,点
,点 在抛物线
在抛物线 上,且
上,且 到
到 的距离比
的距离比 到直线
到直线 的距离小1.
的距离小1.(1)求抛物线
 的方程;
的方程;(2)若点
 为直线
为直线 上的任意一点,过点
上的任意一点,过点 作抛物线
作抛物线 的切线
的切线 与
与 ,切点分别为
,切点分别为 ,求证:直线
,求证:直线 恒过某一定点.
恒过某一定点. -
科目: 来源: 题型:
查看答案和解析>>【题目】【河南省豫南九校(中原名校)2017届高三下学期质量考评八数学(文)】已知双曲线
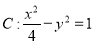 的左右两个顶点是
的左右两个顶点是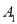 ,
, 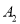 ,曲线
,曲线 上的动点
上的动点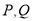 关于
关于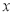 轴对称,直线
轴对称,直线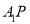 与
与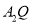 交于点
交于点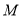 ,
,(1)求动点
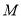 的轨迹
的轨迹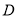 的方程;
的方程;(2)点
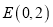 ,轨迹
,轨迹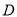 上的点
上的点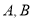 满足
满足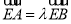 ,求实数
,求实数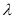 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2016高考浙江文数】如图,设抛物线
 的焦点为F,抛物线上的点A到y轴的距离等于|AF|-1.
的焦点为F,抛物线上的点A到y轴的距离等于|AF|-1. 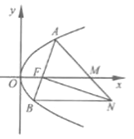
(I)求p的值;
(II)若直线AF交抛物线于另一点B,过B与x轴平行的直线和过F与AB垂直的直线交于点N,AN与x
轴交于点M.求M的横坐标的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 【2016高考新课标Ⅲ文数】已知抛物线
 :
: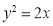 的焦点为
的焦点为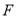 ,平行于
,平行于 轴的两条直线
轴的两条直线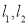 分别交
分别交 于
于 两点,交
两点,交 的准线于
的准线于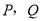 两点.
两点.(I)若
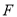 在线段
在线段 上,
上,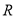 是
是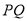 的中点,证明
的中点,证明 ;
;(II)若
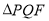 的面积是
的面积是 的面积的两倍,求
的面积的两倍,求 中点的轨迹方程.
中点的轨迹方程.
相关试题

