【题目】已知函数![]() (
(![]() ,
, ![]() )为奇函数,且相邻两对称轴间的距离为
)为奇函数,且相邻两对称轴间的距离为![]() .
.
(1)当![]() 时,求
时,求![]() 的单调递减区间;
的单调递减区间;
(2)将函数![]() 的图象沿
的图象沿![]() 轴方向向右平移
轴方向向右平移![]() 个单位长度,再把横坐标缩短到原来的
个单位长度,再把横坐标缩短到原来的![]() (纵坐标不变),得到函数
(纵坐标不变),得到函数![]() 的图象.当
的图象.当![]() 时,求函数
时,求函数![]() 的值域.
的值域.
参考答案:
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)由题意,化简得到![]() ,根据相邻量对称轴间的距离求得函数的最小正周期,进而得到
,根据相邻量对称轴间的距离求得函数的最小正周期,进而得到![]() 的值,根据奇函数,求解
的值,根据奇函数,求解![]() ,得到函数的解析式,进而求解函数的单调区间即可;
,得到函数的解析式,进而求解函数的单调区间即可;
(2)根据三角函数的图象变换得到![]() 的解析式,根据题意求解
的解析式,根据题意求解![]()
的取值范围,即可求解函数的值域.
试题解析:
(1)由题意可得: ![]() ,
,
因为相邻量对称轴间的距离为![]() ,所以
,所以![]() ,
, ![]() ,
,
因为函数为奇函数,所以![]() ,
, ![]() ,
, ![]() ,
,
因为![]() ,所以
,所以![]() ,函数
,函数![]()
∵![]() ∴
∴![]()
要使![]() 单调减,需满足
单调减,需满足![]() ,
, ![]()
所以函数的减区间为![]() ;
;
(2)由题意可得: ![]()
∵![]() ,∴
,∴![]()
∴![]() ,∴
,∴![]()
即函数![]() 的值域为
的值域为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a∈R,函数f(x)=
 +alnx﹣3x,g(x)=﹣x2+8x,且x=1是函数f(x)的极大值点.
+alnx﹣3x,g(x)=﹣x2+8x,且x=1是函数f(x)的极大值点.
(1)求a的值.
(2)如果函数y=f(x)和函数y=g(x)在区间(b,b+1)上均为增函数,求实数b的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设a>0,
 是R上的函数,且满足f(﹣x)=f(x),x∈R.
是R上的函数,且满足f(﹣x)=f(x),x∈R.
(1)求a的值;
(2)证明f(x)在(0,+∞)上是增函数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 ,其中a>0,且函数f(x)的最大值是
,其中a>0,且函数f(x)的最大值是 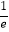
(1)求实数a的值;
(2)若函数g(x)=lnf(x)﹣b有两个零点,求实数b的取值范围;
(3)若对任意的x∈(0,2),都有f(x)<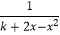 成立,求实数k的取值范围.
成立,求实数k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数y=f(x)的定义域是[0,4],则函数g(x)=
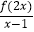 的定义域是( )
的定义域是( )
A.[0,2]
B.[0,2)
C.[0,1)∪(1,2]
D.[0,4] -
科目: 来源: 题型:
查看答案和解析>>【题目】为调查了解某省属师范大学师范类毕业生参加工作后,从事的工作与教育是否有关的情况,该校随机调查了该校80位性别不同的2016年师范类毕业大学生,得到具体数据如下表:
与教育有关
与教育无关
合计
男
30
10
40
女
35
5
40
合计
65
15
80
(1)能否在犯错误的概率不超过5%的前提下,认为“师范类毕业生从事与教育有关的工作与性别有关”?
参考公式:
 (
( ).
).附表:

0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010

0.455
0.708
1.323
2.072
2.706
3.841
5.023
6.635
(2)求这80位师范类毕业生从事与教育有关工作的频率;
(3)以(2)中的频率作为概率.该校近几年毕业的2000名师范类大学生中随机选取4名,记这4名毕业生从事与教育有关的人数为
 ,求
,求 的数学期望
的数学期望 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)的最小值为1,且f(0)=f(2)=3.
(1)求f(x)的解析式;
(2)若f(x)在区间[2a,a+1]上不单调,求实数a的取值范围;
(3)在区间[﹣1,1]上,y=f(x)的图象恒在y=2x+2m+1的图象上方,试确定实数m的取值范围.
相关试题

