【题目】已知a∈R,函数f(x)= ![]() +alnx﹣3x,g(x)=﹣x2+8x,且x=1是函数f(x)的极大值点.
+alnx﹣3x,g(x)=﹣x2+8x,且x=1是函数f(x)的极大值点.
(1)求a的值.
(2)如果函数y=f(x)和函数y=g(x)在区间(b,b+1)上均为增函数,求实数b的取值范围.
参考答案:
【答案】
(1)解:因为函数 ![]() (x>0)
(x>0)
所以f′(x)=x+ ![]() ﹣3,(x>0),
﹣3,(x>0),
又因为x=1是函数f(x)的极大值点.
所以 ![]() ,解得a=2
,解得a=2
检验:当a=2时, ![]() (x>0)
(x>0)
当x∈(0,1),(2,+∞)时,f′(x)>0,当x∈(1,2)时,f′(x)<0,
所以x=1是函数f(x)的极大值点,a=2符合题意
(2)解:g(x)=﹣x2+8x=﹣(x﹣4)2+16
所以函数g(x)的单调递增区间是(4,+∞)
又由(1)可知函数f(x)的单调递增区间是(0,1),(2,+∞)
所以依题意得 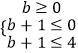 或
或 ![]()
解得 b=0或 2≤b≤3
所以实数b的取值范围是{0}∪[2,3]
【解析】(1)因为函数 ![]() (x>0),求出导函数,利用x=1是函数f(x)的极大值点.求出a.然后验证即可.(2)求出函数g(x)的单调递增区间.又由(1)可知函数f(x)的单调递增区间是(0,1),(2,+∞),列出不等式组,求解b 的范围即可.
(x>0),求出导函数,利用x=1是函数f(x)的极大值点.求出a.然后验证即可.(2)求出函数g(x)的单调递增区间.又由(1)可知函数f(x)的单调递增区间是(0,1),(2,+∞),列出不等式组,求解b 的范围即可.
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的极值与导数的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 的外接圆半径
的外接圆半径 ,角A、B、C的对边分别是a、b、c,且
,角A、B、C的对边分别是a、b、c,且 .
. (I)求角B和边长b;
(II)求
 面积的最大值及取得最大值时的a、c的值,并判断此时三角形的形状.
面积的最大值及取得最大值时的a、c的值,并判断此时三角形的形状. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数中表示同一函数的是( )
A.y= 与y=(
与y=( 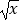 )4
)4
B.y=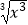 与y=
与y= 
C.y= ?与y=
?与y= 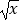 ?
? 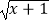
D.y= 与y=
与y= 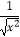
-
科目: 来源: 题型:
查看答案和解析>>【题目】正三棱柱
 的底边长为2,
的底边长为2, 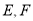 分别为
分别为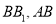 的中点.
的中点.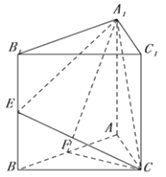
(1)已知
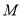 为线段
为线段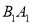 上的点,且
上的点,且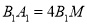 ,求证:
,求证: 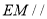 面
面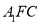 ;
;(2)若二面角
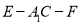 的余弦值为
的余弦值为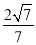 ,求
,求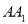 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设a>0,
 是R上的函数,且满足f(﹣x)=f(x),x∈R.
是R上的函数,且满足f(﹣x)=f(x),x∈R.
(1)求a的值;
(2)证明f(x)在(0,+∞)上是增函数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 ,其中a>0,且函数f(x)的最大值是
,其中a>0,且函数f(x)的最大值是 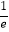
(1)求实数a的值;
(2)若函数g(x)=lnf(x)﹣b有两个零点,求实数b的取值范围;
(3)若对任意的x∈(0,2),都有f(x)<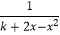 成立,求实数k的取值范围.
成立,求实数k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( ,
,  )为奇函数,且相邻两对称轴间的距离为
)为奇函数,且相邻两对称轴间的距离为 .
.(1)当
 时,求
时,求 的单调递减区间;
的单调递减区间;(2)将函数
 的图象沿
的图象沿 轴方向向右平移
轴方向向右平移 个单位长度,再把横坐标缩短到原来的
个单位长度,再把横坐标缩短到原来的 (纵坐标不变),得到函数
(纵坐标不变),得到函数 的图象.当
的图象.当 时,求函数
时,求函数 的值域.
的值域.
相关试题

