【题目】为调查了解某省属师范大学师范类毕业生参加工作后,从事的工作与教育是否有关的情况,该校随机调查了该校80位性别不同的2016年师范类毕业大学生,得到具体数据如下表:
与教育有关 | 与教育无关 | 合计 | |
男 | 30 | 10 | 40 |
女 | 35 | 5 | 40 |
合计 | 65 | 15 | 80 |
(1)能否在犯错误的概率不超过5%的前提下,认为“师范类毕业生从事与教育有关的工作与性别有关”?
参考公式:![]() (
(![]() ).
).
附表:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.023 | 6.635 |
(2)求这80位师范类毕业生从事与教育有关工作的频率;
(3)以(2)中的频率作为概率.该校近几年毕业的2000名师范类大学生中随机选取4名,记这4名毕业生从事与教育有关的人数为![]() ,求
,求![]() 的数学期望
的数学期望![]() .
.
参考答案:
【答案】(1)见解析;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】试题分析:(1)计算观测值![]() ,即可得出结论;
,即可得出结论;
(2)由图表中的数据计算这80位师范类毕业生从事与教育有关工作的频率;
(3)由题意知X服从B(4, ![]() ), 计算均值E(X)即可.
), 计算均值E(X)即可.
试题解析:(1)根据列联表计算观测值
![]() ,
,
因为K2<3.841,
所以在犯错误的概率不超过5%的前提下,
不能认为“师范类毕业生从事与教育有关的工作与性别有关”;
(2)由图表知这80位师范类毕业生从事与教育有关工作的频率为
![]() ;
;
(3)由题意知X服从B(4, ![]() ),
),
则E(X)=np=4×![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 ,其中a>0,且函数f(x)的最大值是
,其中a>0,且函数f(x)的最大值是 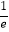
(1)求实数a的值;
(2)若函数g(x)=lnf(x)﹣b有两个零点,求实数b的取值范围;
(3)若对任意的x∈(0,2),都有f(x)<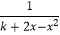 成立,求实数k的取值范围.
成立,求实数k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( ,
,  )为奇函数,且相邻两对称轴间的距离为
)为奇函数,且相邻两对称轴间的距离为 .
.(1)当
 时,求
时,求 的单调递减区间;
的单调递减区间;(2)将函数
 的图象沿
的图象沿 轴方向向右平移
轴方向向右平移 个单位长度,再把横坐标缩短到原来的
个单位长度,再把横坐标缩短到原来的 (纵坐标不变),得到函数
(纵坐标不变),得到函数 的图象.当
的图象.当 时,求函数
时,求函数 的值域.
的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数y=f(x)的定义域是[0,4],则函数g(x)=
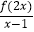 的定义域是( )
的定义域是( )
A.[0,2]
B.[0,2)
C.[0,1)∪(1,2]
D.[0,4] -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)的最小值为1,且f(0)=f(2)=3.
(1)求f(x)的解析式;
(2)若f(x)在区间[2a,a+1]上不单调,求实数a的取值范围;
(3)在区间[﹣1,1]上,y=f(x)的图象恒在y=2x+2m+1的图象上方,试确定实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数f(x)是偶函数,且在(﹣∞,0]上是增函数,又f(2)=0,则xf(x)>0的解集是( )
A.(﹣2,2)
B.(﹣∞,﹣2)∪(0,2)
C.(﹣∞,﹣2)∪(2,+∞)
D.(﹣2,0]∪(2,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】若A={x|2x≤(
 )x﹣2},则函数y=(
)x﹣2},则函数y=(  )x(x∈A)的值域为 .
)x(x∈A)的值域为 .
相关试题

