【题目】若函数f(x)=  ,则函数y=|f(x)|﹣
,则函数y=|f(x)|﹣ ![]() 的零点个数为 .
的零点个数为 .
参考答案:
【答案】4
【解析】解:当x≥1时, ![]() =
= ![]() ,即lnx=
,即lnx= ![]() , 令g(x)=lnx﹣
, 令g(x)=lnx﹣ ![]() ,x≥1时函数是连续函数,
,x≥1时函数是连续函数,
g(1)=﹣ ![]() <0,g(2)=ln2﹣
<0,g(2)=ln2﹣ ![]() =ln
=ln ![]() >0,
>0,
g(4)=ln4﹣2<0,由函数的零点判定定理可知g(x)=lnx﹣ ![]() ,有2个零点.
,有2个零点.
(结合函数y= ![]() 与y=
与y= ![]() 可知函数的图象由2个交点.)
可知函数的图象由2个交点.)
当x<1时,y= 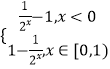 ,函数的图象与y=
,函数的图象与y= ![]() 的图象如图,考查两个函数由2个交点,
的图象如图,考查两个函数由2个交点,
综上函数y=|f(x)|﹣ ![]() 的零点个数为:4个.
的零点个数为:4个.
故答案为:4.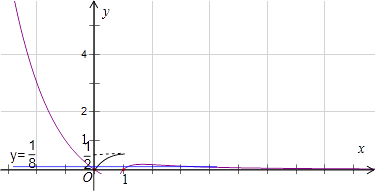
利用分段函数,对x≥1,通过函数的零点与方程根的关系求解零点个数,当x<1时,利用数形结合求解函数的零点个数即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若
 ,
,  ,则实数
,则实数 的取值范围为__________.
的取值范围为__________.【答案】

【解析】当m=0时,符合题意。
当m≠0时,
 ,则0<m<4,
,则0<m<4,则0m<4
答案为:
 .
.点睛:解本题的关键是处理二次函数在区间上大于0的恒成立问题,对于二次函数的研究一般从以几个方面研究:
一是,开口;
二是,对称轴,主要讨论对称轴与区间的位置关系;
三是,判别式,决定于x轴的交点个数;
四是,区间端点值.
【题型】填空题
【结束】
15【题目】已知椭圆
 :
:  的右焦点为
的右焦点为 ,
,  为直线
为直线 上一点,线段
上一点,线段 交
交 于点
于点 ,若
,若 ,则
,则 __________.
__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
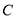 :
: 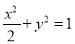 的右焦点为
的右焦点为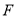 ,
, 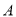 为直线
为直线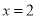 上一点,线段
上一点,线段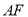 交
交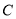 于点
于点 ,若
,若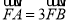 ,则
,则 __________.
__________.【答案】
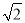
【解析】
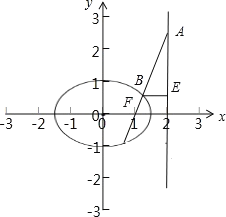
由条件椭圆
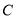 :
: 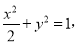 ∴
∴
椭圆的右焦点为F,可知F(1,0),
设点A的坐标为(2,m),则
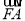 =(1,m),
=(1,m),∴
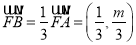 ,
,∴点B的坐标为
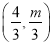 ,
,∵点B在椭圆C上,
∴
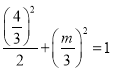 ,解得:m=1,
,解得:m=1,∴点A的坐标为(2,1),
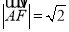 .
.答案为:
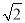 .
.【题型】填空题
【结束】
16【题目】四棱锥
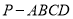 中,
中, 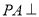 面
面 ,
,  是平行四边形,
是平行四边形, 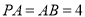 ,
, 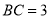 ,点
,点 为棱
为棱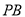 的中点,点
的中点,点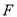 在棱
在棱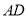 上,且
上,且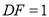 ,平面
,平面 与
与 交于点
交于点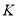 ,则异面直线
,则异面直线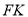 与
与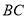 所成角的正切值为__________.
所成角的正切值为__________. -
科目: 来源: 题型:
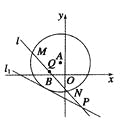
查看答案和解析>>【题目】(本小题满分13分)如图所示,已知以点
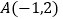 为圆心的圆与直线
为圆心的圆与直线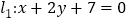 相切.过点
相切.过点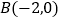 的动直线
的动直线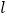 与圆
与圆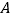 相交于
相交于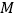 ,
,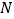 两点,
两点,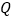 是
是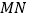 的中点,直线
的中点,直线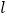 与
与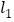 相交于点
相交于点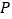 .
.
(1)求圆
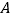 的方程;
的方程;(2)当
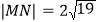 时,求直线
时,求直线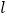 的方程.
的方程.(3)
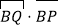 是否为定值?如果是,求出其定值;如果不是,请说明理由.
是否为定值?如果是,求出其定值;如果不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】四棱锥
 中,
中,  面
面 ,
,  是平行四边形,
是平行四边形,  ,
, 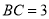 ,点
,点 为棱
为棱 的中点,点
的中点,点 在棱
在棱 上,且
上,且 ,平面
,平面 与
与 交于点
交于点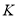 ,则异面直线
,则异面直线 与
与 所成角的正切值为__________.
所成角的正切值为__________.【答案】

【解析】

延长
 交
交 的延长线与点Q,连接QE交PA于点K,设QA=x,
的延长线与点Q,连接QE交PA于点K,设QA=x,由
 ,得
,得 ,则
,则 ,所以
,所以 .
.取
 的中点为M,连接EM,则
的中点为M,连接EM,则 ,
,所以
 ,则
,则 ,所以AK=
,所以AK= .
.由AD//BC,得异面直线
 与
与 所成角即为
所成角即为 ,
,则异面直线
 与
与 所成角的正切值为
所成角的正切值为 .
.【题型】填空题
【结束】
17【题目】在极坐标系中,极点为
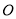 ,已知曲线
,已知曲线 :
:  与曲线
与曲线 :
:  交于不同的两点
交于不同的两点 ,
,  .
.(1)求
 的值;
的值;(2)求过点
 且与直线
且与直线 平行的直线
平行的直线 的极坐标方程.
的极坐标方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】纹样是中国艺术宝库的瑰宝,火纹是常见的一“种传统纹样.为了测算某火纹纹样(如图阴影部分所示)的面积,作一个边长为
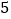 的正方形将其包含在内,并向该正方形内随机投掷
的正方形将其包含在内,并向该正方形内随机投掷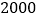 个点,已知恰有
个点,已知恰有 个点落在阴影部分,据此可估计阴影部分的面积是( )
个点落在阴影部分,据此可估计阴影部分的面积是( )
A.
 B.
B. 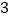 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列
 和等比数列
和等比数列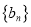 满足
满足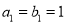 ,
,  ,
,  .
.(1)求
 的通项公式;
的通项公式;(2)求和:
 .
.【答案】(1)
 ;(2)
;(2) .
.【解析】试题分析:(1)根据等差数列
 的
的 ,
,  ,列出关于首项
,列出关于首项 、公差
、公差 的方程组,解方程组可得
的方程组,解方程组可得 与
与 的值,从而可得数列
的值,从而可得数列 的通项公式;(2)利用已知条件根据题意列出关于首项
的通项公式;(2)利用已知条件根据题意列出关于首项 ,公比
,公比 的方程组,解得
的方程组,解得 、
、 的值,求出数列
的值,求出数列 的通项公式,然后利用等比数列求和公式求解即可.
的通项公式,然后利用等比数列求和公式求解即可.试题解析:(1)设等差数列{an}的公差为d. 因为a2+a4=10,所以2a1+4d=10.解得d=2.
所以an=2n1.
(2)设等比数列的公比为q. 因为b2b4=a5,所以b1qb1q3=9.
解得q2=3.所以
 .
.从而
 .
.【题型】解答题
【结束】
18【题目】已知命题
 :实数
:实数 满足
满足 ,其中
,其中 ;命题
;命题 :方程
:方程 表示双曲线.
表示双曲线.(1)若
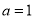 ,且
,且 为真,求实数
为真,求实数 的取值范围;
的取值范围;(2)若
 是
是 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围.
相关试题

