【题目】已知椭圆![]() :
: ![]() 的右焦点为
的右焦点为![]() ,
, ![]() 为直线
为直线![]() 上一点,线段
上一点,线段![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() __________.
__________.
【答案】![]()
【解析】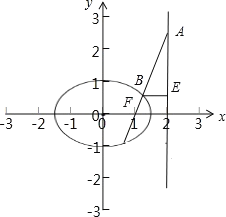
由条件椭圆![]() :
: ![]() ∴
∴![]()
椭圆的右焦点为F,可知F(1,0),
设点A的坐标为(2,m),则![]() =(1,m),
=(1,m),
∴![]() ,
,
∴点B的坐标为![]() ,
,
∵点B在椭圆C上,
∴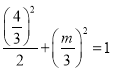 ,解得:m=1,
,解得:m=1,
∴点A的坐标为(2,1),![]() .
.
答案为: ![]() .
.
【题型】填空题
【结束】
16
【题目】四棱锥![]() 中,
中, ![]() 面
面![]() ,
, ![]() 是平行四边形,
是平行四边形, ![]() ,
, ![]() ,点
,点![]() 为棱
为棱![]() 的中点,点
的中点,点![]() 在棱
在棱![]() 上,且
上,且![]() ,平面
,平面![]() 与
与![]() 交于点
交于点![]() ,则异面直线
,则异面直线![]() 与
与![]() 所成角的正切值为__________.
所成角的正切值为__________.
参考答案:
【答案】![]()
【解析】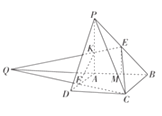
延长![]() 交
交![]() 的延长线与点Q,连接QE交PA于点K,设QA=x,
的延长线与点Q,连接QE交PA于点K,设QA=x,
由![]() ,得
,得![]() ,则
,则![]() ,所以
,所以![]() .
.
取![]() 的中点为M,连接EM,则
的中点为M,连接EM,则![]() ,
,
所以![]() ,则
,则![]() ,所以AK=
,所以AK=![]() .
.
由AD//BC,得异面直线![]() 与
与![]() 所成角即为
所成角即为![]() ,
,
则异面直线![]() 与
与![]() 所成角的正切值为
所成角的正切值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点
 到点
到点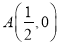 ,
, 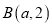 及到直线
及到直线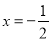 的距离都相等,如果这样的点恰好只有一个,那么实数
的距离都相等,如果这样的点恰好只有一个,那么实数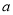 的值是( )
的值是( )A.
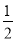 B.
B. 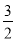 C.
C.  或
或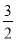 D.
D. 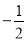 或
或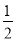
【答案】D
【解析】试题分析:由题意知
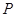 在抛物线
在抛物线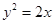 上,设
上,设 ,则有
,则有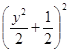
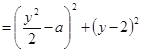 ,化简得
,化简得 ,当
,当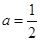 时,符合题意;当
时,符合题意;当 时,
时,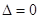 ,有
,有 ,
,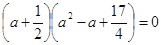 ,则
,则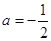 ,所以选D.
,所以选D.考点:1、点到直线的距离公式;2、抛物线的性质.
【方法点睛】本题考查抛物线的概念、性质以及数形结合思想,属于中档题,到点
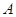 和直线
和直线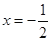 的距离相等,则
的距离相等,则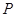 的轨迹是抛物线,再由直线与抛物线的位置关系可求;抛物线的定义是解决物线问题的基础,它能将两种距离(抛物线上的点到到焦点的距离、抛物线上的点到准线的距离)进行等量转化,如果问题中涉及抛物线的焦点和准线,又能与距离联系起来,那么用抛物线的定义就能解决.
的轨迹是抛物线,再由直线与抛物线的位置关系可求;抛物线的定义是解决物线问题的基础,它能将两种距离(抛物线上的点到到焦点的距离、抛物线上的点到准线的距离)进行等量转化,如果问题中涉及抛物线的焦点和准线,又能与距离联系起来,那么用抛物线的定义就能解决.【题型】单选题
【结束】
13【题目】在极坐标系中,已知两点
 ,
, 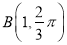 ,则
,则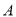 ,
, 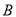 两点间的距离为__________.
两点间的距离为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】一台风中心在港口南偏东
 方向上,距离港口
方向上,距离港口 千米处的海面上形成,并以每小时
千米处的海面上形成,并以每小时 千米的速度向正北方向移动,距台风中心
千米的速度向正北方向移动,距台风中心 千米以内的范围将受到台风的影响,则港口受到台风影响的时间为( )
千米以内的范围将受到台风的影响,则港口受到台风影响的时间为( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】若
 ,
,  ,则实数
,则实数 的取值范围为__________.
的取值范围为__________.【答案】

【解析】当m=0时,符合题意。
当m≠0时,
 ,则0<m<4,
,则0<m<4,则0m<4
答案为:
 .
.点睛:解本题的关键是处理二次函数在区间上大于0的恒成立问题,对于二次函数的研究一般从以几个方面研究:
一是,开口;
二是,对称轴,主要讨论对称轴与区间的位置关系;
三是,判别式,决定于x轴的交点个数;
四是,区间端点值.
【题型】填空题
【结束】
15【题目】已知椭圆
 :
:  的右焦点为
的右焦点为 ,
,  为直线
为直线 上一点,线段
上一点,线段 交
交 于点
于点 ,若
,若 ,则
,则 __________.
__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分13分)如图所示,已知以点
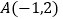 为圆心的圆与直线
为圆心的圆与直线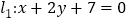 相切.过点
相切.过点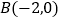 的动直线
的动直线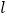 与圆
与圆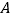 相交于
相交于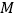 ,
,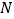 两点,
两点,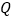 是
是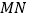 的中点,直线
的中点,直线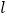 与
与 相交于点
相交于点 .
.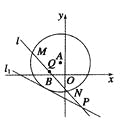
(1)求圆
 的方程;
的方程;(2)当
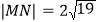 时,求直线
时,求直线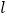 的方程.
的方程.(3)
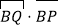 是否为定值?如果是,求出其定值;如果不是,请说明理由.
是否为定值?如果是,求出其定值;如果不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数f(x)=
 ,则函数y=|f(x)|﹣
,则函数y=|f(x)|﹣  的零点个数为 .
的零点个数为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】四棱锥
 中,
中,  面
面 ,
,  是平行四边形,
是平行四边形,  ,
, 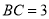 ,点
,点 为棱
为棱 的中点,点
的中点,点 在棱
在棱 上,且
上,且 ,平面
,平面 与
与 交于点
交于点 ,则异面直线
,则异面直线 与
与 所成角的正切值为__________.
所成角的正切值为__________.【答案】

【解析】

延长
 交
交 的延长线与点Q,连接QE交PA于点K,设QA=x,
的延长线与点Q,连接QE交PA于点K,设QA=x,由
 ,得
,得 ,则
,则 ,所以
,所以 .
.取
 的中点为M,连接EM,则
的中点为M,连接EM,则 ,
,所以
 ,则
,则 ,所以AK=
,所以AK= .
.由AD//BC,得异面直线
 与
与 所成角即为
所成角即为 ,
,则异面直线
 与
与 所成角的正切值为
所成角的正切值为 .
.【题型】填空题
【结束】
17【题目】在极坐标系中,极点为
 ,已知曲线
,已知曲线 :
:  与曲线
与曲线 :
:  交于不同的两点
交于不同的两点 ,
,  .
.(1)求
 的值;
的值;(2)求过点
 且与直线
且与直线 平行的直线
平行的直线 的极坐标方程.
的极坐标方程.
相关试题

