【题目】如图是某市3月1日至14日的空气质量指数趋势图.空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染.某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.
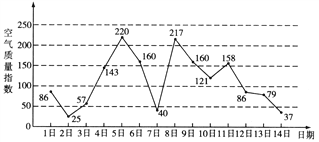
(Ⅰ)求此人到达当日空气重度污染的概率;
(Ⅱ)设X是此人停留期间空气质量优良的天数,求X的分布列与数学期望;
(Ⅲ)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)
参考答案:
【答案】(Ⅰ) ![]() ;(Ⅱ)答案见解析;(Ⅲ)从3月5日开始连续三天的空气质量指数方差最大.
;(Ⅱ)答案见解析;(Ⅲ)从3月5日开始连续三天的空气质量指数方差最大.
【解析】试题分析:(1)先确定空气重度污染日,再根据古典概型概率公式求概率为![]() ,(2)先确定随机变量取法,再分别求对应概率,最后根据数学期望公式求期望,(3) 方差最大,即数据变化幅度最大,由图可得结论.
,(2)先确定随机变量取法,再分别求对应概率,最后根据数学期望公式求期望,(3) 方差最大,即数据变化幅度最大,由图可得结论.
试题解析:设Ai表示事件“此人于3月i日到达该市”(i=1,2,…,13).
根据题意, ![]() ,且
,且![]()
(Ⅰ)设B为事件“此人到达当日空气重度污染”,则![]() .
.
∴![]()
(Ⅱ)由题意可知,X的所有可能取值为0,1,2,且
![]() ,
,
![]()
![]()
∴X的分布列为:
X | 0 | 1 | 2 |
P |
|
|
|
故X的数学期望![]()
(Ⅲ)从3月5日开始连续三天的空气质量指数方差最大
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
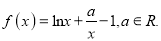
(1)若曲线
 在点
在点 处的切线与直线
处的切线与直线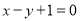 垂直,求函数的极值;
垂直,求函数的极值;(2)设函数
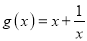 .当
.当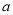 =
=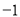 时,若区间[1,e]上存在x0,使得
时,若区间[1,e]上存在x0,使得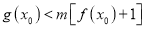 ,求实数
,求实数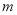 的取值范围.(
的取值范围.(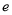 为自然对数底数)
为自然对数底数) -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,曲线
中,曲线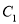 的参数方程为
的参数方程为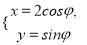 (
( 为参数),在以
为参数),在以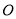 为极点,
为极点,  轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线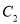 是圆心为
是圆心为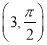 ,半径为1的圆.
,半径为1的圆.(1)求曲线
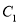 ,
, 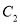 的直角坐标方程;
的直角坐标方程;(2)设
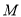 为曲线
为曲线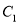 上的点,
上的点, 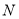 为曲线
为曲线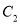 上的点,求
上的点,求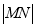 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P-ABCD中, PA⊥平面ABCD,E为BD的中点,G为PD的中点,△DAB≌△DCB,EA=EB=AB=1,
 ,连接CE并延长交AD于F.
,连接CE并延长交AD于F.(Ⅰ)求证:AD⊥CG;
(Ⅱ)求平面BCP与平面DCP的夹角的余弦值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,椭圆的中心为原点O,长轴在x轴上,离心率
 ,过左焦点F1作x轴的垂线交椭圆于A,
,过左焦点F1作x轴的垂线交椭圆于A, 两点
两点 .
.(Ⅰ)求该椭圆的标准方程;
(Ⅱ)取垂直于x轴的直线与椭圆相交于不同的两点P,
 ,过P、
,过P、 作圆心为Q的圆,使椭圆上的其余点均在圆Q外.若
作圆心为Q的圆,使椭圆上的其余点均在圆Q外.若 ,求圆Q的标准方程.
,求圆Q的标准方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
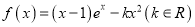 .
.(Ⅰ)当
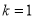 时,求函数
时,求函数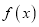 的单调区间;
的单调区间;(Ⅱ)当
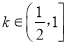 时,求函数
时,求函数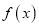 在
在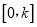 上的最大值M.
上的最大值M. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2018广东省深中、华附、省实、广雅四校联考】已知椭圆
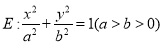 的离心率为
的离心率为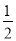 ,圆
,圆 与
与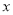 轴交于点
轴交于点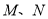 ,
, 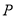 为椭圆
为椭圆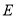 上的动点,
上的动点,  ,
, 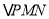 面积最大值为
面积最大值为 .
.(I)求圆
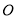 与椭圆
与椭圆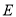 的方程;
的方程;(II)圆
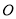 的切线
的切线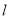 交椭圆于点
交椭圆于点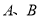 ,求
,求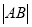 的取值范围.
的取值范围.
相关试题

